各种组学分析技术的进展导致了我们在收集数据时更侧重数据信息的保存,然而我们收集的数据最终也会根据我们的想探索的问题来寻找答案,甚至有时候我们在实验设计分组时就打算考察某一个变量而为了获取更多的相关信息而采用了组学技术。这点是尤其要强调的,科研人员一定是面向科学问题解决科学问题,而不要为了应用新技术而应用新技术。当然,现实的情况是新技术特别是组学技术的发展为我们提供了大量的可同时测定的生物学指标(例如基因表达水平、蛋白表达水平、代谢产物表达水平)数据,大到我们事先也不知道会有什么模式会出现,这样就需要数据挖掘,特别是统计学知识来帮助我们发现新知。然而,组学技术产生的这类高通量数据是具有一些特质的,数据里确实会有我们关心分组的差异表达,但同时也有大量测量值对于我们设定的分组不敏感,然而当我们去对比组间差异时就会被这些数据干扰。
举例而言,我对两组样品(暴露组跟对照组)中每一个样品测定了10000个指标,每组有10个样品,那么如果我想知道差异有多大就需要对比10000次,具体说就是10000次双样本t检验。那么如果我对t检验的置信水平设置在0.05,也就是5%假阳性,做完这10000次检验,我会期望看到500个假阳性,而这500个有显著差异的指标其实对分组不敏感也可以随机生成。假如真实测到了600个有显著差异的指标,那么如何区分其中哪些是对分组敏感?哪些又仅仅只是随机的呢?随机的会不会只有500个整呢?
这就是多重检验问题,做经典科研实验时往往会忽略,深层次的原因是经典的科研实验往往是理论或经验主导需要进行检验的假说。例如,我测定血液中白血球的数目就可以知道你是不是处于炎症中,其背后是医学知识的支撑。然而,再组学或其他高通量实验中,研究实际是数据导向的,也就是不管有用没用反正我测了一堆指标,然后就去对比差异,然后就是上面的问题了,我们可能分不清楚哪些是真的相关,哪些又是随机出现的。
当然这个问题出现也不是一天两天了,再多重比较问题上就已经被提出过,只不过在多重比较里对比数因为排列组合比较多而在多重检验里纯粹就是因为同时进行的假设检验数目多。那么其实从统计角度解决的方法也基本来源于此。
整体错误率(Family-wise error rate)控制
对于单次比较,当我们看到显著差异的p值脑子里想的是空假设为真时发生的概率,当我们置信水平设定在0.95(I型错误率0.05)而p值低于对应的阈值,那么我们应该拒绝空假设。但对比次数多了从概率上就会出现已经被拒绝的假设实际是错误的而你不知道是哪一个。整体错误率控制的思路就是我不管单次比较了,我只对你这所有的对比次数的总错误率进行控制。还是上面的例子,对于10000次假设检验我只能接受1个错误,整体犯错概率为0.0001,那么对于单次比较,其I型错误率也得设定在这个水平上去进行假设检验,结果整体上错误率是控制住了,但对于单次比较就显得十分严格了。下面用一个仿真实验来说明:
# 随机数的10000次比较
set.seed(42)
pvalue <- NULL
for (i in 1:10000){
a <- rnorm(10)
b <- rnorm(10)
c <- t.test(a,b)
pvalue[i] <- c$p.value
}
# 看下p值分布
hist(pvalue)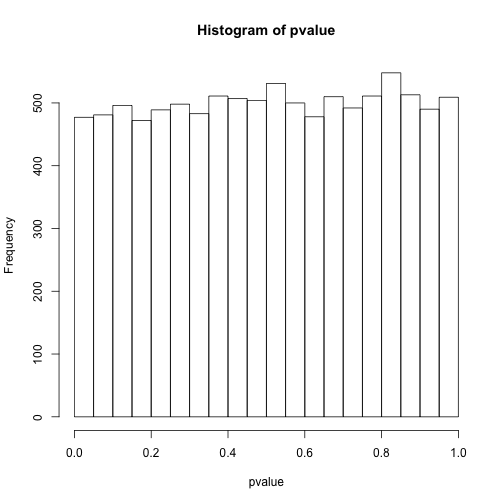
plot of chunk null
# 小于0.05的个数
sum(pvalue<0.05)## [1] 477# 小于0.0001的个数
sum(pvalue<0.0001)## [1] 0这样我们会看到进行了整体的控制之后,确实是找不到有差异的了,但假如里面本来就有有差异的呢?
set.seed(42)
pvalue <- NULL
for (i in 1:10000){
a <- rnorm(10,1)
b <- a+1
c <- t.test(a,b)
pvalue[i] <- c$p.value
}
# 看下p值分布
hist(pvalue)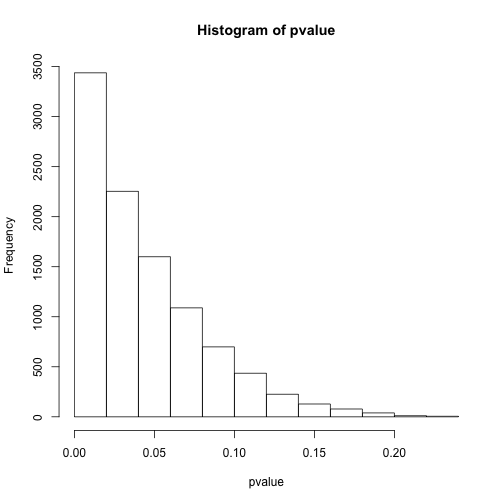
plot of chunk diff
# 小于0.05的个数
sum(pvalue<0.05)## [1] 6559# 小于0.0001的个数
sum(pvalue<0.0001)## [1] 45上面我们模拟了10000次有真实差异的假设检验,结果按照单次检验0.05的阈值能发现约7000有差异,而使用0.0001却只能发现不到100次有显著差异。那么问题很明显,或许控制整体错误率可以让我们远离假阳性,但假阴性也就是II型错误率就大幅提高了,最后的结果可能是什么差异也看不到。
下面我们尝试一个更实际的模拟,混合有差异跟无差异的检验:
set.seed(42)
pvalue <- NULL
for (i in 1:5000){
a <- rnorm(10,1)
b <- a+1
c <- t.test(a,b)
pvalue[i] <- c$p.value
}
for (i in 1:5000){
a <- rnorm(10,1)
b <- rnorm(10,1)
c <- t.test(a,b)
pvalue[i+5000] <- c$p.value
}
# 看下p值分布
hist(pvalue)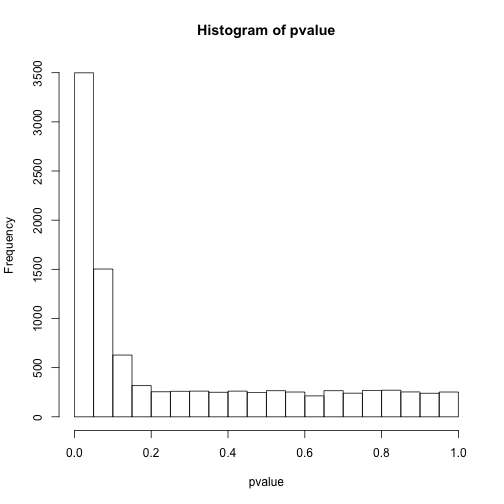
plot of chunk mix
# 小于0.05的个数
sum(pvalue<0.05)## [1] 3499# 小于0.0001的个数
sum(pvalue<0.0001)## [1] 21此时结果就更有意思了,明明应该有5000次是有差异的,但阈值设定在0.05只能看到约3500次,而0.0001只能看到24次。
上面的模拟告诉我们,降低假阳性会提高假阴性的比率,而且似乎本来0.05的阈值对于真阳性也是偏小的。同时,面对假设检验概率低于0.05的那些差异,我们也没有很好的方法区别哪些是真的,哪些是随机的。
其实很多人都知道整体错误率控制是比较严格的,但也不是完全没人用,例如寻找生物标记物做重大疾病诊断时就不太能接受假阳性而可以接受一定的假阴性,此时如果标准放宽就会找到一大堆假信号,到时候标记不准就会对诊断产生负面影响。
下面介绍下常见的整体错误率控制方法:
Bonferroni 方法
思路很简单,就是控制显著性,例如单次检验假阳性比率\(\alpha\)控制在0.05,那么n次检验假阳性比率控制为\(\frac{\alpha}{n}\)。这样实际是对整体采用了个体控制的控制思路:
\[ P(至少一个显著)=1-P(无显著差异) = 1-(1-\alpha/n)^n \]
我们来看下\(\alpha = 0.05\)随比较数增加的效果:
n <- c(1:10 %o% 10^(1:2))
p0 <- 1-(1-0.05)^n
p <- 1-(1-0.05/n)^n
# 不进行控制
plot(p0~n,ylim = c(0,1))
# Bonferroni方法控制
points(p~n,pch=19)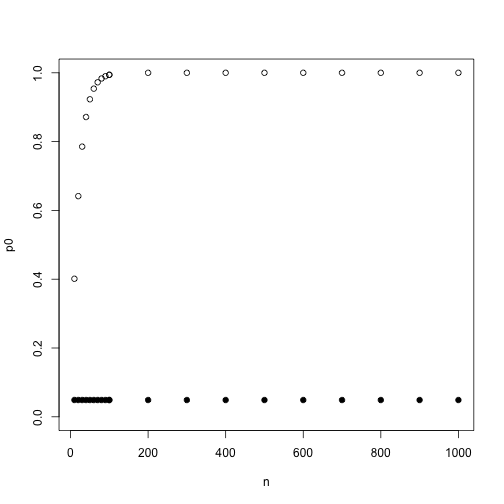
plot of chunk Bonferroni
其实,这样的控制得到的整体错误率是略低于0.05的,并且数目越大,整体错误率越低。这个方法十分保守,有可能什么差异你都看不到,因为都变成假阴性了。在实际应用中一般不调节p值的假阳性比率而直接调节p值,取原始p值跟整体检验数目的乘积与1的最小值作为调节p值,还可以用0.05或0.01进行判断,不过这时候控制的整体而不是单一检验了。
当然这只是最原始的Bonferroni方法,后来Holm改进了这种一步法为逐步法,此时我们需要首先对原始p值进行排序,然后每个原始p值乘上其排序作为调节p值。例如三次多重检验的p值分别是0.01、0.03与0.06,其调节后的p值为0.03,0.06,0.06。如果我们控制整体假阳性比率低于0.05,那么调解后只有第一个检验可以拒绝空假设。值得注意的是Holm的改进是全面优于原始方法的,也就是说当你一定要去用Bonferroni方法控制整体错误率,优先选Holm的改进版。
Sidak 方法
上面那种方法其实有点非参的意思,其实数学上我们是可以精确的把假阳性比率控制在某个数值的:
\[ P(至少一个显著)=1-P(无显著差异) = 1-(1-\alpha')^n = 0.05 \]
求解可得到\(\alpha' = 1-0.95^{\frac{1}{n}}\),此时我们就可以比较精确的控制整体错误率了,但是,这个方法有个前提就是各个检验必须是独立的,这在生物学实验里几乎不可能,所以这个方法的应用远没有Bonferroni方法广。
错误发现率(False Discovery Rate)控制
刚才的模拟中我们可以看到,控制整体错误率比较严格,假阴性比率高,那么有没有办法找到假阴性比率低的呢?要知道我们其实只关心有差异的那部分中那些是真的,哪些是假的,无差异的可以完全不用考虑。那么我们可以尝试控制错误发现率,也就是在有差异的那一部分指标中控制错误率低于某一水平。
# 所有有差异的
R <- sum(pvalue<0.05)
# 假阳性
V <- sum(pvalue[5001:10000]<0.05)
# 错误发现率
Q <- V/R
R## [1] 3499V## [1] 225Q## [1] 0.06430409上面的计算显示虽然我们漏掉了很多阳性结果,但错误发现率并不高。事实上如果我们控制错误率到0.01,错误发现率会更低:
# 所有有差异的
R <- sum(pvalue<0.01)
# 假阳性
V <- sum(pvalue[5001:10000]<0.01)
# 错误发现率
Q <- V/R
R## [1] 999V## [1] 34Q## [1] 0.03403403其实出现这个问题不难理解,空假设检验里p值是均匀分布的而有差异检验的p值是有偏分布且偏向于较小的数值,所以假阳性控制的越小,有偏分布占比例就越高,但同时会造成假阴性提高的问题。
那么错误发现率会不会比整体错误率的控制更好呢?这里通过两种常见的控制方法进行说明。
Benjamini-Hochberg方法
这个方法跟Holm方法很像,也是先排序,但之后p值并不是简单的乘排序,而是乘检验总数后除排序:
\[ p_i \leq \frac{i}{m} \alpha \]
举例来说就是假设三次多重检验的p值分别是0.01、0.03与0.06,其调节后的p值为0.03,0.045,0.06。那么为什么说这种方法控制的是错误发现率呢?我们来看下\(\alpha\)是如何得到的:p值乘总数m得到的是在该p值下理论发现数,而除以其排序实际是该p值下实际发现数,理论发现数基于在这里的分布是均匀分布,也就是空假设的分布,这两个的比值自然就是错误发现率。下面我用仿真实验来说明一下:
pbh <- p.adjust(pvalue,method = 'BH')
ph <- p.adjust(pvalue,method = 'holm')
plot(pbh~pvalue)
points(ph~pvalue,col='red')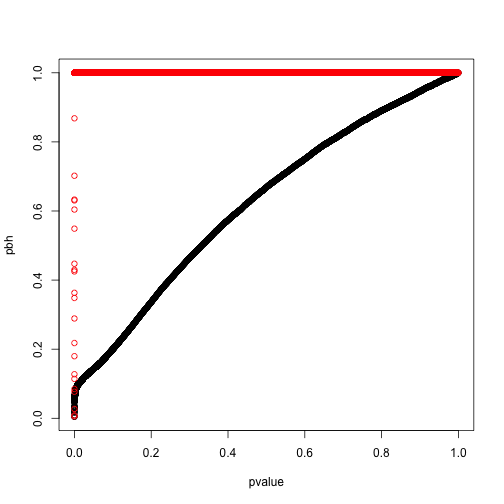
plot of chunk BH
从上面图我们可以看出,如果控制整体错误率(红色),那么p值很容易就到1了,过于严格。而如果用BH方法控制错误发现率,那么原始p值越大,调节后的错误发现率也逐渐递增,这就符合了区分真实差异与随机差异就要假设真实差异更可能出现更小的p值这个现象。当然至于这个方法的推演细节,可以去读原始论文。值得注意的是这个错误发现率求的是有差异存在的情况,不然零发现就出现除数为零了。
Storey方法(q值)
如果说BH方法还算是调节了p值,那么Storey提出的方法则直接去估计了错误发现率本身。刚才介绍BH算法时我提到总数m与p值的乘积是基于这里的分布是均匀分布,但实际上按照错误发现率的定义,这里应该出现的是空假设总数。直接使用所有检验数会造成一个问题,那就是对错误发现率的高估,为了保证功效,这里应该去估计空假设的总体比例。这里我们去观察混合分布会发现在p值较大的时候基本可以认为这里分布的都是空假设的p值,那么我们可以用:
\[ \hat\pi_0 = \frac{\#\{p_i>\lambda\}}{(1-\lambda)m} \]
估计这个比例\(\hat\pi_0\),其中参数\(\lambda\)的跟\(\hat\pi_0\)的关系可以用一个三阶方程拟合,然后计算出整体假阳性比例。有了这个比例,我们再去按照BH方法计算p值,然后两个相乘就会得到q值,而q值的理论含义就是在某一概率上低于这个概率所有数里假阳性的比重。打个比方,我测到某个指标的q值是0.05,这意味着q值低于这个数所有检验中我有0.05的可能性得到的是假阳性。。但我们会发现当空假设比重较高时BH结果跟q值很接近,而比重很低的话q值会变得更小,功效会提高,基本也符合我们对错误发现率的预期。
library(qvalue)
q <- qvalue(pvalue)
# Q值
plot(q$qvalues~pvalue,col='blue')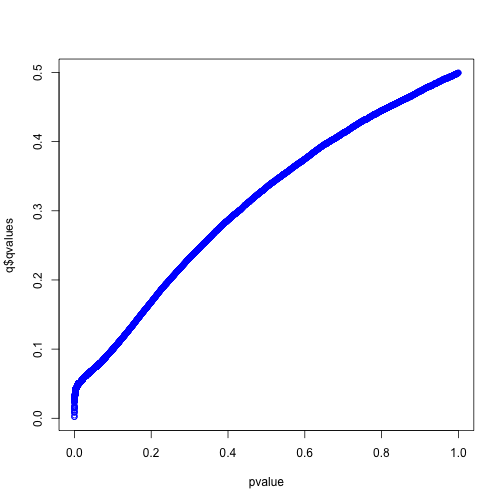
plot of chunk qvalues
如上图所示,q值增大后会最终逼近到0.5,而我们的模拟中空假设的比例就设定就是50%。我们重新模拟一个空假设比例5%的实验:
set.seed(42)
pvalue <- NULL
for (i in 1:500){
a <- rnorm(10,1)
b <- a+1
c <- t.test(a,b)
pvalue[i] <- c$p.value
}
for (i in 1:9500){
a <- rnorm(10,1)
b <- rnorm(10,1)
c <- t.test(a,b)
pvalue[i+500] <- c$p.value
}
pbh <- p.adjust(pvalue,method = 'BH')
ph <- p.adjust(pvalue,method = 'holm')
q <- qvalue(pvalue)
plot(pbh~pvalue)
# Holm 方法
points(ph~pvalue,col='red')
# Q值
points(q$qvalues~pvalue,col='blue')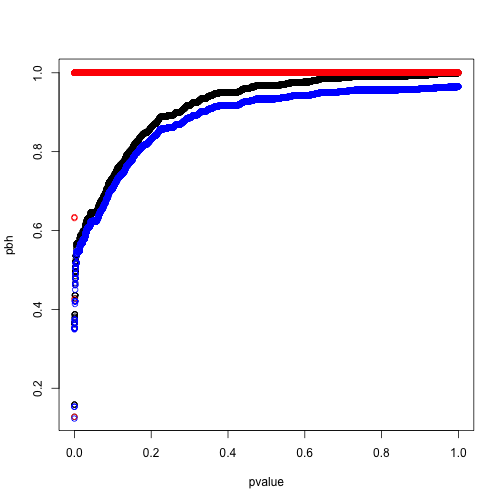
plot of chunk qbh
此时我们可以看到两者结果较为接近,q值理论上更完备,功效也更强,但算法上对\(\hat\pi_0\)的估计并不稳定,特别是比例靠近1的时候,所以BH方法可能还是更容易让人接受的保守错误发现率控制。详细的估计方法还得去啃Storey的论文。
小结
多重检验问题是高通量数据里逃不掉的问题,要想找出真正的差异数据就要面对假阳性跟假阴性问题,这是一个不可兼得的过程,看重假阳性就用整体错误率,看重功效就用错误发现率控制。并不是说哪种方法会好一些,更本质的问题在于你对实际问题的了解程度及统计方法的适用范围。例如你选基因芯片时实际也进行了一次选择,改变了整体检验的p值分布,而不同的p值分布对应的处理方法也不太一样,有兴趣可以读下这篇。有时候你的实验设计本身就会影响数据的统计行为,而这个恰恰是最容易被忽视的。