先从最简单的例子来,假设我们比较两组人的平均身高该如何做?我们要对两组人采样,采样数最好一样,然后测量每个样本的身高,记录后分组计算均值与方差。如果目的是比较均值,那么首先要考虑使用的方法,如果是t检验,那么先对均值的方差进行F检验来确定是否需要等方差t检验,然后就是双样本t检验,结果显著(p<0.05)我们就说这两组人的身高有显著性差异(无差异就是0),给出两组身高的均值与差异的置信区间,我们的数据分析就完了。上述过程槽点略多,不吐槽了,如果你在实验室一线至少要掌握上面那个实验设计与数据分析的思路来寻找差异,多数科学发现的本质就是寻找未知的差异。
下面是一组R代码,模拟了两组数据均值的对比,读懂输出的结果,另外注意R默认的t检验是不等方差的。
# 模拟生成两组数据
group1 <- rnorm(100,100,10)
group2 <- rnorm(100,130,13)
# 进行t检验
t.test(group1,group2)
# 结果
# Welch Two Sample t-test
#
#data: group1 and group2
#t = -16.857, df = 186.154,
#p-value < 2.2e-16
#alternative hypothesis: true difference in means is not equal to 0
#95 percent confidence interval:
# -30.50828 -24.11558
#sample estimates:
#mean of x mean of y
# 100.9668 128.2787
如果是基因组数据分析,基本思路就是设定实验组与对照组,对比找出差异,对有差异的数据在相应物种基因组里定位然后寻找功能注释,后面就是讲故事阶段了。但不同于我们对比身高,基因组数据分析对比的不单单是一组变量例如身高,而是一堆变量例如基因A,B,C,D,……,Z。当然不止26个,这时我们遇到的问题就是一个样本,几百上千维的描述如何保证样本代表性。这个问题的解决一般要靠实验设计,对比差异的话至少也要有两组,每组多少生物学重复通过试验来检测下统计功效,在满足一定功效的前提下反推需要的样本数。
在基因芯片表达谱这个矩阵上,我们希望得到的信息是高度依赖所研究的科学问题的。大概有如下这两种:
-
我的样本不分组,都是得了一种恶性病,我想找出这种病在基因层次的描述。这种情况你需要采集样本的基因组数据,对样本基因表达谱进行聚类,找出变化相对一致的基因。
-
我在实验设计就有两组数据,这种情况可以直接对这两组进行t检验,然后对差异基因进行数据库检索或功能定位,进而依据组别判断数据的生物学意义。
照这样看似乎并不难,本质上就是跟对照或数据库的数据找差异,可以看作是t检验的推广。但问题实际比想象的要复杂,举例而言,两组样本每个样本测定1000个基因,在0.05置信区间上至少出现50个假阳性,更何况一般芯片测的数比这要多,而常识上多数基因是不受影响的,也就是即便假阳性比率不高,但只要有就会影响我们回答科学问题。下面我用模拟数据来说明下这个问题。
# 安装bioconductor
source("http://bioconductor.org/biocLite.R")
biocLite()
# genefilter包用来同时进行高维t检验,得到所有基因的分组差异
# Biobase包用来提供处理表达数据集的方法
# biocLite('genefilter')
library(genefilter)
library(Biobase)
# GSE5859数据集收集了不同人种的基因表达数据
# devtools::install_github("genomicsclass/GSE5859")
library(GSE5859)
# 读入数据
data(GSE5859)
# 提取分组信息,这里先选取两个人种
info <- pData(e)
g <- info$ethnicity
gASNCEU <- which(g == 'ASN' | g == 'CEU')
group <- factor(g[gASNCEU])
# 提取表达谱原始数据
exp <- exprs(e)[,gASNCEU]
# 进行分组t检验
results <- rowttests(exp,group)
# 提取结果p值
pvals <- results$p.value
# 模拟随机表达谱并提取p值
m <- nrow(exp)
n <- ncol(exp)
randomData <- matrix(rnorm(n*m),m,n)
nullresults <- rowttests(randomData,group)
nullpvals <- nullresults$p.value
# 随机分组比较并提取p值
permg <- sample(group)
permresults <- rowttests(exp,permg)
permpvals <- permresults$p.value
# 观察p值分布与火山图
par(mfrow = c(2,3))
hist(pvals,ylim=c(0,9000))
hist(permpvals,ylim=c(0,9000))
hist(nullpvals,ylim=c(0,9000))
plot(results$dm,-log10(pvals),
xlab="Effect size",ylab="- log (base 10) p-values")
plot(permresults$dm,-log10(permpvals),
xlab="Effect size",ylab="- log (base 10) p-values")
plot(nullresults$dm,-log10(nullpvals),
xlab="Effect size",ylab="- log (base 10) p-values")
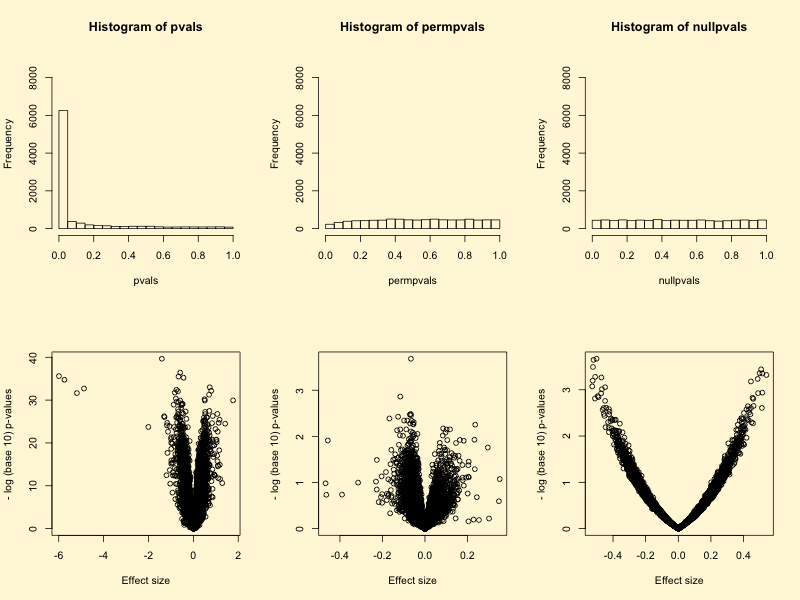
从上面的分析我们可以看出p值的分布在实际样品与随机数据是有差异的。随机数据中p值的分布是均匀分布,但样品中明显是偏态分布,而且火山图可以看出均值差较小时出现了很多有显著性差异的数值。毋庸置疑,这会干扰我们后续的通路分析。
数据也就长这样了,问题就是多次比较后假阳性比较多。我们可以用比较保守的Bonferroni矫正来用比较小的p值控制假阳性,当然为了保证统计功效,也可以使用控制错误发现率的方法来减少假阳性。一般控制错误发现率都是针对全局的,但q值法提供了一种对每个对比进行检验的方法,当q值比较小,我们认为这个结果还是比较靠谱的。这样当一个基因同时满足q值与p值小于0.05,那么我们大概可以说这组数的差异是显著的,我们也筛到了想要的基因。
另一个更常用的解决方法是使用经验贝叶斯方法。我们注意看一下随机数据生成的火山图,这里面与实际数据相比差异与p值大致趋势一致。当我们假设多数基因应该是不变化时,我们就应该同时收敛差异与p值的离散状况。这里我们假设各组基因的变化服从一个超分布,然后计算t值时对方差进行贝叶斯加权。当基因组内差异小其方差权重小而整体权重大,当差异大时整体权重小,这样就实现了t值的一个收敛,最后给出的火山图也跟着收敛了。经验贝叶斯方法算是基因组数据分析里比较常用的方法,单看效果应该不错,可以配合q值去筛选差异基因。
下一篇我们从t检验推广到线性模型,并想办法矫正掉一些批次效应。