如果说线性模型是科研里用得最多的数据分析模型,那么非线性模型大概是科研忽悠用语里的常客了。理解线性模型一张XY散点图加上一条笔直的视觉引导线就足够讲清楚线性回归效应了,但前面加上个“非”字就是另一番风景了,这只说明两个变量间的关系没法用Y = aX+b来描述,但能用什么模型来描述就没法从名字里看出来了。那么,今天就来聊聊如何描述非线性。
还是从实际问题出发,我测定了某种污染物甲在某区域不同采样点检出的浓度,本质上就是得到了表示浓度的一维向量。现在我怀疑这个浓度跟某个工厂有关系,如何描述这个关系,最直观就是计算所有采样点到工厂的距离,然后拟合一个模型:
浓度 = f(距离)
这里f代表描述这两个变量间关系的模型,最简单的模型就是浓度是不变的常数,那么方程可以写为:
浓度 = 系数*距离^0 + 常数
其实这里有没有距离都无所谓,反正0次方都是1,但考虑到就算是常数也会有测量误差,这个模型可以写成:
浓度 = 系数*距离^0 + 常数 + 误差
误差会符合正态分布,因此要验证这个模型是否靠谱,我们需要做的就是对测量的浓度进行拟合优度检验看是否符合正态分布,如果符合,那就说明我们提出的常数模型靠谱,这里跟距离可能没有关系。这个模型虽然最简单,但经常会被忽略,毕竟搞研究的总是在寻找变量间的关系而不是检验单变量的随机性。
但是不是过了常数模型就一定没关系呢?不一定,单一变量正态分布更可能说明采样足够随机但不说明没有其他因素可以解释,这里我们让模型复杂一点:
浓度 = 系数*距离^1+常数+误差
这就是最常见的线性模型了,此时我们认为浓度被距离所影响,拟合这个模型后会得到系数及对这个系数的检验,此处的检验目的就是看这个系数与零有没有统计意义上的显著差异,如果有,那么这个模型很可能捕捉到了两个变量间的关系。如果没差异,那么距离前这个系数就可能是零,也就是退回常数模型。有差异时把拟合的线画出来就是一条描述两变量关系的直线,例如距离越远,浓度越低。
然而,虽然线性模型捕捉到了两个变量间的关系,但不代表这个关系的描述就一定是最好的。例如,我们注意到当距离越远,浓度下降越快。从地理常识上这很容易解释,污染物在二维平面扩散一定是越远浓度下降越快,复杂点也就是所谓高斯扩散模型。注意这个模型是个指数模型,已经是非线性了,但不是说没法用线性模型来拟合。在没有物理机制模型的时候,线性模型总是探索分析的第一选择。
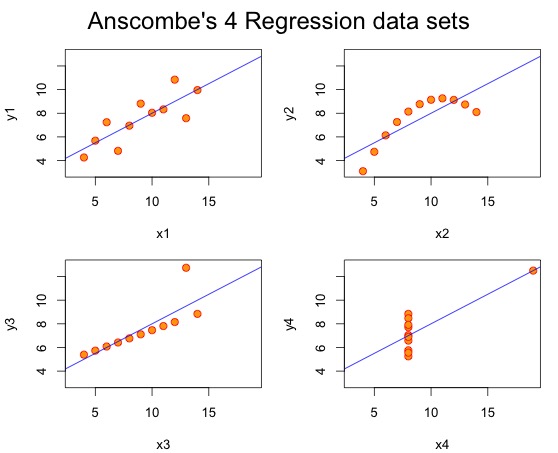
此处可视化是很重要的,例如下图里的安斯库姆四重奏,其回归线都是一样的,R2也是一样的,单纯看数据分析的结果是无法识别数据本身的状态的。
现在我们可以继续让模型复杂一点,例如我们假设跟距离的平方成正比,也就是:
浓度 = 系数*距离^2+常数+误差
此时我们假设的就是一个非线性模型,具体来说就是多项式模型。如前所述,如果你知道两个变量间物理机制,那么机制模型是最准的。但如果不知道机制,多项式模型可以作为一种优先探索模型,原因是纯数学上的,任何函数理论上都可以用多项式模型来近似,也就是传说中的泰勒展开。然而,这个泰勒展开只是一种数值方法,不能用其直接反推数据背后的机理。
此时,我们又发现,在距离近似相等的采样点上,温度越高浓度越低,也就是我们这里要考虑两个自变量:
浓度 = 系数1*距离^2+系数2*温度 + 常数+误差
这里就是单纯的加性模型,用来说明固定其余自变量时,某自变量对因变量的影响。这个模型最常见的就是在流行病学里对协变量的控制,例如当文章里说在控制了性别、年龄、BMI、是否抽烟后某个行为对疾病发病率的影响,其实质就是构建一个多元加性模型,把性别、年龄、BMI、抽烟与否等跟某个行为都作为自变量累加到一起来决定因变量,拟合后行为前的系数就是控制了其他因素后的影响。在这个加性模型里,自变量可以是连续变量,也可以是离散变量,当自变量是离散变量时,本质上就是拟合不同离散变量下的模型,因此如果你全是离散变量,很可能遇到维度诅咒,也就是某些自变量组合下数据不足,此时就要考虑换模型了,毕竟眼下这个模型理论上就会训练不足。当然,每一个自变量都可以进行多项式展开,但多项式越多,需要拟合的参数也越多,也就更可能训练不足,此时模型也会更复杂,微小变化就会产生很大影响。由于科研里寻找的模型都是尽量重现性高预测性好的,提高复杂度很可能降低模型对新数据的预测性,此时要谨慎判断,例如你可以加1/2次方而不是2次方,此时参数虽然也是多,但不容易累积微弱影响。另外,模型越简单越好解释,参数量要远小于数据量更可能给出靠谱结果(奥卡姆剃刀)。
此时,我们需要考虑一个更复杂的场景,这个场景下距离跟温度存在交互作用,距离远了温度影响会变大,而近了污染源距离影响更大,此时模型就可以表述为:
浓度 = 系数3*温度*距离 + 常数+误差
这里我们可以用另一种表述方法来描述,也就是网络法:
距离 -> 温度 -> 浓度
在网络表示中,类似距离 -> 温度 -> 浓度这种表达在数学上的意义就是乘法法则,也就是距离跟温度的交互作用就是其单独影响的乘积。打比方距离增加1,温度减少2,而温度减少1,浓度提高3,此时距离增加1,浓度提高就是2*3,也就是6,因此我们在模型里会直接用两个自变量乘积表示交互作用,此时也在暗示自变量之间可能存在某种互相作用机制。当我们在一个线性模型里加入了自变量互相作用项时,本质上就是在说自变量间的信息会影响因变量。例如,我们发现就业二十年的收入跟原生家庭收入与入学考试分数的交互作用有关,当原生家庭收入碰上高分,收入会突然增高,此时我们就可以合理推测原生家庭收入本身可能就跟入学考试分数之间有关系,例如家庭收入高更可能请私教。当然,这是从解释性角度来讨论模型,如果你研究的现象机理模型已经很成熟了,那直接拟合就可以了。
交互作用也属于非线性模型了,还有一些非线性则属于分段式函数。但实际科研里八成现象可以用线性模型解决,剩下的一成可以用多项式与乘法互相作用解决,用到其他数学表达的场景那一成大都是由学科理论支撑的公式。绝大多数情况下,科研里理解透了线性模型就够用了,大多数新发现都是用线性模型来描述与解释的。
当然,我说的是机器学习模型出现之前的科研数据分析里的线性与非线性,下次聊一下另一个常见数据分析模型:层级模型。