这是我最近研究工作中遇到的一个有趣现象:有一组含对照与控制样本的多维数据在主成分分析里没有看到差异,但进行差异分析时发现几乎所有维度上都有差异。这就会形成解释数据上的悖论:如果我用主成分分析来进行探索式数据分析,会认为对照组与控制组很难区分;但如果我用单一维度的差异分析去对比,即使经过错误发现率控制,在绝大多数维度上都能看到差异。这里的问题在于,因为你每个维度上都显示了差异,按说整体降维后可视化差异应该很明显才对。那么,这两组数据究竟算有差异还是没差异?
这里我用模拟仿真来重现下这个问题。首先,我们模拟两组数据,对照组与控制组均有100维,都存在1.2倍均值差异,每组十万个点:
library(genefilter)
# 100个维度
np <- rnorm(100,100,100)
z <- c()
for(i in 1:100){
case <- rnorm(100000,mean = np[i],sd=abs(np[i])*0.1+1)
control <- rnorm(100000,mean=np[i]*1.2,sd=abs(np[i])*0.1+1)
zt <- c(case,control)
z <- cbind(z,zt)
}我们来看下主成分分析结果:
pca <- prcomp(z)
# 主成分贡献
summary(pca)$importance[,c(1:10)]## PC1 PC2 PC3 PC4 PC5 PC6
## Standard deviation 139.6394 32.62823 30.70480 29.50805 28.36421 26.82567
## Proportion of Variance 0.4811 0.02627 0.02326 0.02148 0.01985 0.01775
## Cumulative Proportion 0.4811 0.50736 0.53062 0.55211 0.57196 0.58971
## PC7 PC8 PC9 PC10
## Standard deviation 23.62678 23.19695 22.98213 22.70652
## Proportion of Variance 0.01377 0.01328 0.01303 0.01272
## Cumulative Proportion 0.60348 0.61676 0.62979 0.64251plot(pca$x[,1],pca$x[,2],pch=19,col=c(rep(1,100000),rep(2,100000)))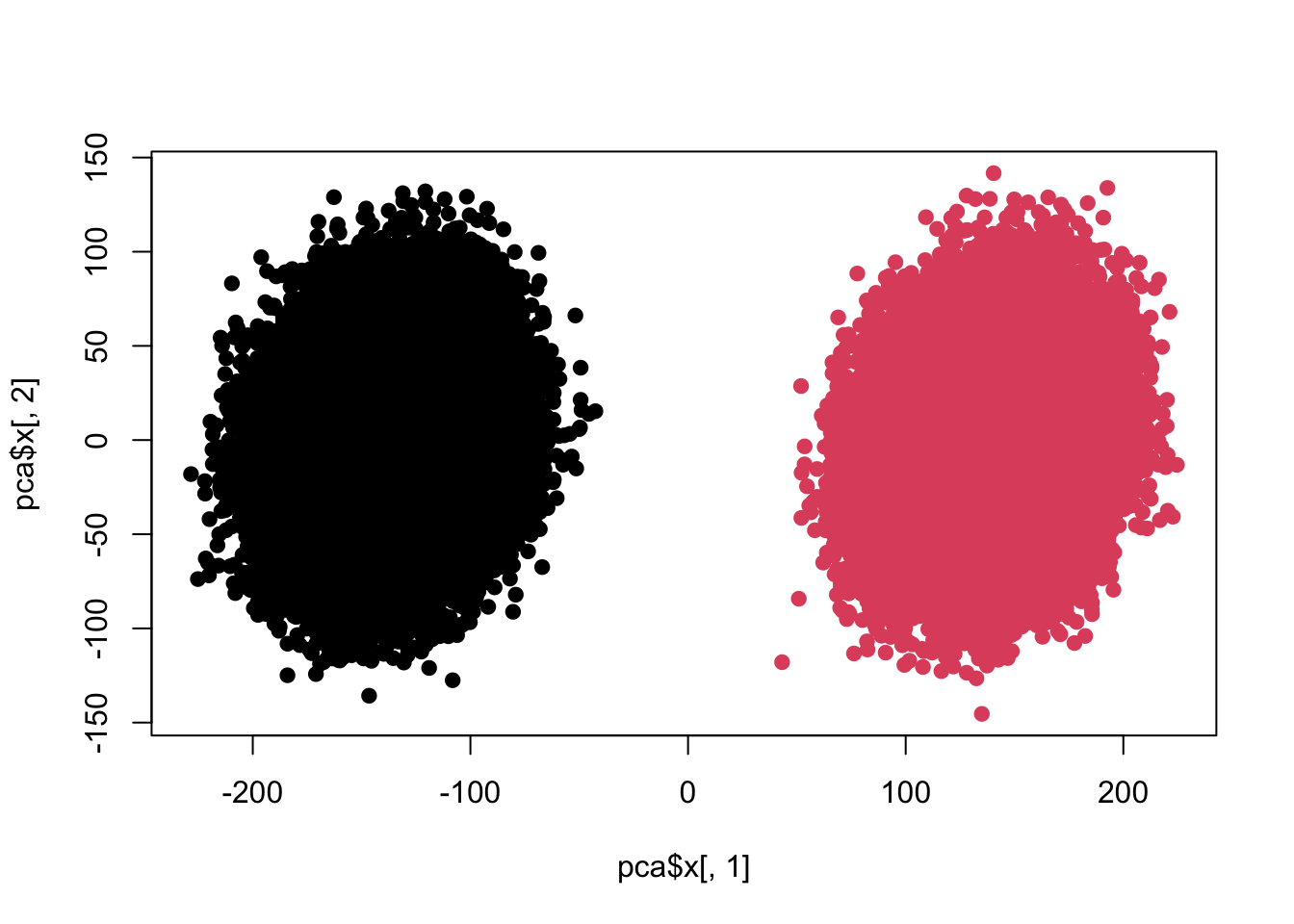
colnames(z) <- 1:ncol(z)
re <- colttests(z,factor(c(rep(1,100000),rep(2,100000))))
re$adj <- p.adjust(re$p.value,'BH')
sum(re$adj<0.05)## [1] 100很明显差异。下面我们要做些变化:
z <- c()
for(i in 1:100){
case <- rnorm(100000,mean = np[i],sd=abs(np[i])*0.5+1)
control <- rnorm(100000,mean=np[i]*1.2,sd=abs(np[i])*0.5+1)
zt <- c(case,control)
z <- cbind(z,zt)
}
pca <- prcomp(z)
# 主成分贡献
summary(pca)$importance[,c(1:10)]## PC1 PC2 PC3 PC4 PC5
## Standard deviation 181.57868 157.6794 148.89327 142.83580 135.81297
## Proportion of Variance 0.06511 0.0491 0.04378 0.04029 0.03643
## Cumulative Proportion 0.06511 0.1142 0.15799 0.19828 0.23471
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 127.20252 113.80253 111.40461 110.56104 109.33174
## Proportion of Variance 0.03195 0.02558 0.02451 0.02414 0.02361
## Cumulative Proportion 0.26666 0.29224 0.31674 0.34088 0.36449plot(pca$x[,1],pca$x[,2],pch=19,col=c(rep(1,100000),rep(2,100000)))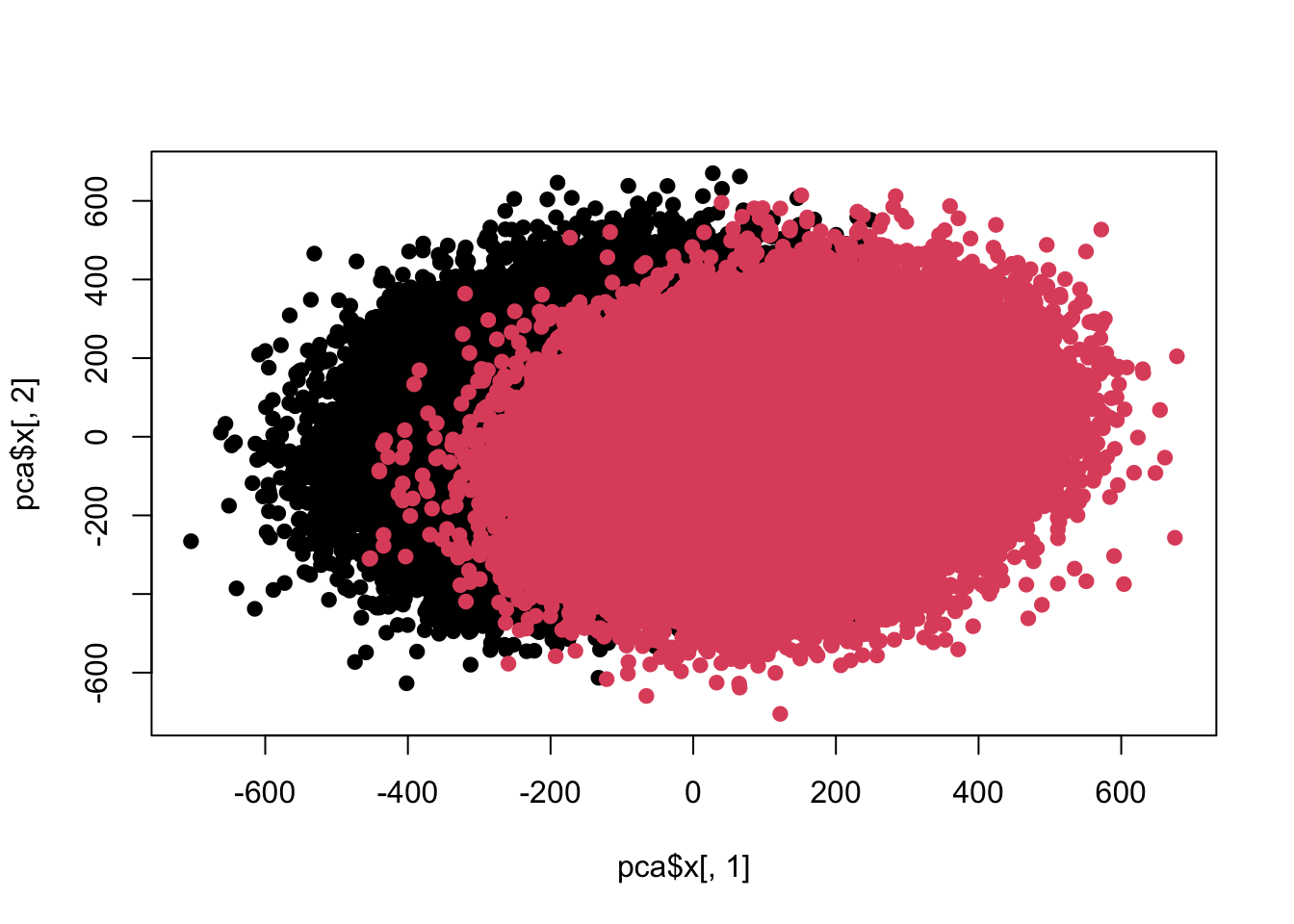
colnames(z) <- 1:ncol(z)
re <- colttests(z,factor(c(rep(1,100000),rep(2,100000))))
re$adj <- p.adjust(re$p.value,'BH')
sum(re$adj<0.05)## [1] 100目前差异已经开始互相融合了,好,进一步加大力度。
z <- c()
for(i in 1:100){
case <- rnorm(100000,mean = np[i],sd=abs(np[i])*1.2+1)
control <- rnorm(100000,mean=np[i]*1.2,sd=abs(np[i])*1.2+1)
zt <- c(case,control)
z <- cbind(z,zt)
}
pca <- prcomp(z)
# 主成分贡献
summary(pca)$importance[,c(1:10)]## PC1 PC2 PC3 PC4 PC5
## Standard deviation 385.92252 362.55544 349.08614 337.24936 318.92927
## Proportion of Variance 0.05343 0.04716 0.04372 0.04081 0.03649
## Cumulative Proportion 0.05343 0.10059 0.14431 0.18512 0.22161
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 276.23167 269.7456 266.37922 264.53726 259.27925
## Proportion of Variance 0.02738 0.0261 0.02546 0.02511 0.02412
## Cumulative Proportion 0.24898 0.2751 0.30055 0.32565 0.34977plot(pca$x[,1],pca$x[,2],pch=19,col=c(rep(1,100000),rep(2,100000)))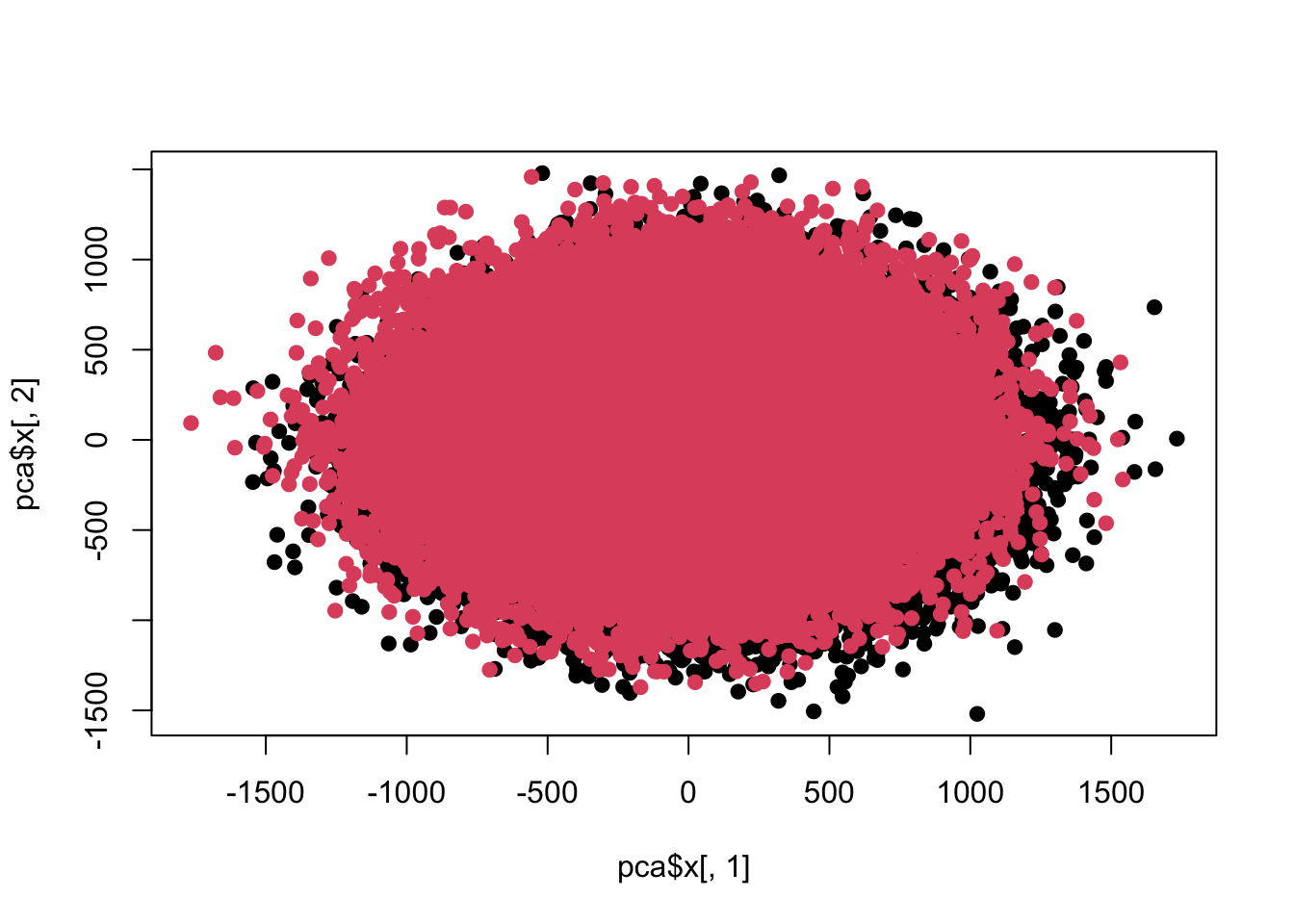
colnames(z) <- 1:ncol(z)
re <- colttests(z,factor(c(rep(1,100000),rep(2,100000))))
re$adj <- p.adjust(re$p.value,'BH')
sum(re$adj<0.05)## [1] 100目前这两组差异数据在前两个主成分上已经看不出来了。
其实这也算不上悖论,主要线索就是主成分的方差贡献,而我做的改动也在相对标准偏差上,第一个是10%,第二个是50%,第三个是120%。也就是说,当单一维度上方差已经大到均值水平时,前几个主成分展示的就不会是本来存在的均值差异。也就是说组内方差已经大于组间方差了,而主成分分析的前几个主成分展示的主要方差的方向,此时就很难看到差异了。
另外一个问题就在为什么每个维度上做t检验都能看到差异?是不是这个检验太灵敏了?这里我们可以换下非参检验试一下:
re <- apply(z, 2, function(x) wilcox.test(x~factor(c(rep(1,100000),rep(2,100000)))))
pv <- sapply(re, function(x) x$p.value)
table(pv)## pv
## 0 3.21613085397256e-306 6.73430585530844e-306
## 6 1 1
## 5.95905672921984e-305 1.43146426990507e-304 2.88103524006124e-304
## 1 1 1
## 3.54613251350956e-304 6.33668140462438e-304 2.5317836364043e-302
## 1 1 1
## 4.93293987160011e-302 8.13835120208514e-302 1.36688105921063e-300
## 1 1 1
## 3.87043506611894e-300 1.33933427039936e-299 6.1328705844548e-299
## 1 1 1
## 6.76244564779203e-299 1.03222194605371e-298 1.51318088864007e-298
## 1 1 1
## 2.11070341524332e-298 6.07875768603152e-297 3.22527514439914e-295
## 1 1 1
## 1.34203144972226e-294 2.10795030613225e-294 8.3934741296955e-294
## 1 1 1
## 1.13524790569676e-293 4.43328524302025e-293 1.13408275302277e-292
## 1 1 1
## 3.21171301670077e-292 9.14432011768732e-292 1.41029103894936e-291
## 1 1 1
## 1.95969386604631e-291 6.81159200573271e-291 9.53869471480568e-291
## 1 1 1
## 3.9974313747202e-289 9.96580693176291e-289 1.18123817159962e-286
## 1 1 1
## 2.91533699652798e-286 4.02616301892293e-286 1.96128094307977e-285
## 1 1 1
## 5.79726146140566e-285 2.17379665526438e-284 8.27240941402517e-284
## 1 1 1
## 1.02270502390125e-283 1.2015695984249e-283 1.27219996005653e-282
## 1 1 1
## 1.33809861944993e-282 1.56263256355399e-282 2.10646448643389e-282
## 1 1 1
## 5.58237541370083e-281 7.35623456436659e-281 2.39983102385879e-280
## 1 1 1
## 4.22036195797059e-280 6.38057745284189e-280 2.59047690236053e-279
## 1 1 1
## 3.85284194755047e-279 3.96545521530779e-279 7.08128308709271e-279
## 1 1 1
## 2.01200858528937e-278 2.70315874477531e-278 2.52529024378762e-277
## 1 1 1
## 2.98489612300307e-277 4.71151481650708e-277 2.71998519646619e-276
## 1 1 1
## 6.89204108667979e-275 7.08424448613288e-275 9.69157985456159e-275
## 1 1 1
## 4.90147598007698e-274 2.10122961611204e-273 5.41706107787206e-273
## 1 1 1
## 1.48806677303251e-272 2.95470348988646e-272 7.0891056275253e-271
## 1 1 1
## 1.19019161487132e-270 9.57399856665466e-270 3.25192278813096e-269
## 1 1 1
## 4.27093134286106e-268 4.83603203666462e-268 1.14715674450228e-265
## 1 1 1
## 2.32625856178469e-265 5.71328484169207e-265 1.03615279334537e-264
## 1 1 1
## 1.32156277038824e-263 1.52458781012718e-262 1.23304701176652e-261
## 1 1 1
## 1.39611670321905e-261 2.42026216418281e-261 4.09109495599137e-260
## 1 1 1
## 2.05071609635835e-259 2.42145196897917e-259 2.20413402311652e-258
## 1 1 1
## 3.43833152538818e-253 3.08137819181166e-252 2.05564214205184e-248
## 1 1 1
## 6.88397114005715e-234 1.04517724949655e-227
## 1 1结果很直观,依然全是差异。那么问题在哪里?其实就是差异本身的性质,这个差异太小,同时样品量又太大,结果这个客观存在的差异就会在大样本的情况下被检验出来。那么皮球就踢回来了,这个微弱但存在的差异有没有物理意义或科学意义?
如果这个差异出现在无关紧要的地方,那么即使有差异可能也没多少意义。打比方我们对比了两个国家的人口拇指指甲宽度,发现其中一个国家的人口拇指指甲平均长度比另一个国家宽0.5毫米。从统计意义上存在显著差异,但实际意义上几乎为零。不过如果这个客观存在的差异有实际意义,那么想用探索式数据分析找到或者发现就不容易了。
什么时候会出现这个问题呢?就是样本量特别大的时候,或者说现在。我们现在把样品量降下来看看:
# 不同样品
n <- c(50,100,1000,5000,10000,50000)
par(mfrow=c(2,3))
for(t in n){
z <- c()
for(i in 1:100){
case <- rnorm(t,mean = np[i],sd=abs(np[i])*1.2+1)
control <- rnorm(t,mean=np[i]*1.2,sd=abs(np[i])*1.2+1)
zt <- c(case,control)
z <- cbind(z,zt)
}
pca <- prcomp(z)
# 主成分贡献
print(summary(pca)$importance[,c(1:10)])
plot(pca$x[,1],pca$x[,2],pch=19,col=c(rep(1,t),rep(2,t)),main=paste(t,'samples'))
colnames(z) <- 1:ncol(z)
re <- colttests(z,factor(c(rep(1,t),rep(2,t))))
re$adj <- p.adjust(re$p.value,'BH')
print(sum(re$adj<0.05))
}## PC1 PC2 PC3 PC4 PC5
## Standard deviation 463.20899 414.93325 390.06915 378.94284 366.74091
## Proportion of Variance 0.07606 0.06104 0.05394 0.05091 0.04768
## Cumulative Proportion 0.07606 0.13710 0.19104 0.24195 0.28963
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 354.55291 333.73123 327.22355 307.45633 294.46379
## Proportion of Variance 0.04456 0.03948 0.03796 0.03351 0.03074
## Cumulative Proportion 0.33419 0.37368 0.41164 0.44515 0.47589## [1] 0
## PC1 PC2 PC3 PC4 PC5
## Standard deviation 414.95519 398.18752 383.1179 341.77149 333.77712
## Proportion of Variance 0.06112 0.05628 0.0521 0.04146 0.03954
## Cumulative Proportion 0.06112 0.11740 0.1695 0.21096 0.25050
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 330.07421 313.23118 295.19766 294.06532 283.41800
## Proportion of Variance 0.03867 0.03483 0.03093 0.03069 0.02851
## Cumulative Proportion 0.28918 0.32400 0.35493 0.38563 0.41414## [1] 3
## PC1 PC2 PC3 PC4 PC5
## Standard deviation 386.36628 372.46631 354.17324 343.27760 329.31797
## Proportion of Variance 0.05329 0.04953 0.04478 0.04207 0.03872
## Cumulative Proportion 0.05329 0.10282 0.14760 0.18967 0.22838
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 286.83421 274.58396 270.4125 267.03231 265.61662
## Proportion of Variance 0.02937 0.02692 0.0261 0.02546 0.02519
## Cumulative Proportion 0.25775 0.28467 0.3108 0.33623 0.36142## [1] 93
## PC1 PC2 PC3 PC4 PC5
## Standard deviation 383.85506 365.76202 350.63025 335.54931 316.81354
## Proportion of Variance 0.05302 0.04814 0.04424 0.04052 0.03612
## Cumulative Proportion 0.05302 0.10117 0.14541 0.18593 0.22205
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 277.27065 269.78110 265.08180 262.41757 259.46220
## Proportion of Variance 0.02767 0.02619 0.02529 0.02478 0.02423
## Cumulative Proportion 0.24971 0.27591 0.30119 0.32597 0.35020## [1] 100
## PC1 PC2 PC3 PC4 PC5
## Standard deviation 389.30440 364.63431 352.40207 334.78785 318.53566
## Proportion of Variance 0.05432 0.04766 0.04451 0.04017 0.03637
## Cumulative Proportion 0.05432 0.10198 0.14649 0.18666 0.22303
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 274.87045 269.58252 265.61018 264.65565 260.47349
## Proportion of Variance 0.02708 0.02605 0.02529 0.02511 0.02432
## Cumulative Proportion 0.25011 0.27616 0.30145 0.32655 0.35087## [1] 100
## PC1 PC2 PC3 PC4 PC5
## Standard deviation 385.48948 362.6262 348.98546 335.73433 319.7928
## Proportion of Variance 0.05333 0.0472 0.04371 0.04046 0.0367
## Cumulative Proportion 0.05333 0.1005 0.14424 0.18470 0.2214
## PC6 PC7 PC8 PC9 PC10
## Standard deviation 276.36173 270.86175 266.40601 263.67463 259.84221
## Proportion of Variance 0.02741 0.02633 0.02547 0.02495 0.02423
## Cumulative Proportion 0.24881 0.27515 0.30062 0.32557 0.34980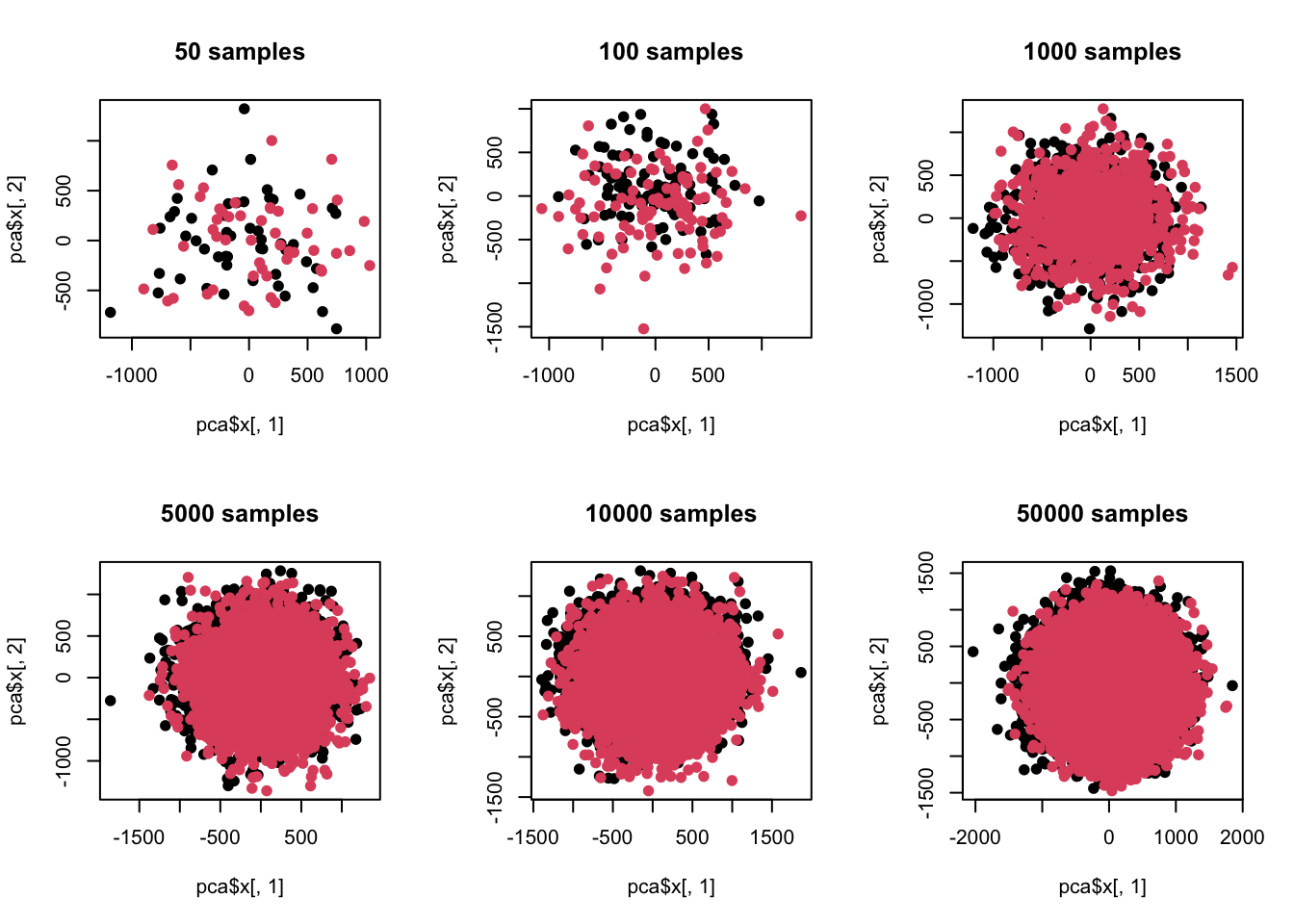
## [1] 100这里我们可以看到,在样品单一维度有差异但方差比较大的情况下,当样品数超过维度后,差异分析跟主成分分析就已经出现灵敏度差异了。也就是说,当样品数增加后,类似主成分分析这种探索式数据分析已经看不出预设差异了。同时我们又注意到,在样品量少于维度时,差异分析功效又是不足的,也就是根本测不到预设差异。
这里有人可能觉得是不是主成分分析只考虑了维度间线性组合,如果我换一种非线性方法会不会还能看到差异?没问题,我们继续模拟:
library(umap)
n <- c(50,100,1000,5000)
par(mfrow=c(2,2))
for(t in n){
z <- c()
for(i in 1:100){
case <- rnorm(t,mean = np[i],sd=abs(np[i])*1.2+1)
control <- rnorm(t,mean=np[i]*1.2,sd=abs(np[i])*1.2+1)
zt <- c(case,control)
z <- cbind(z,zt)
}
umap <- umap(z)
plot(umap$layout,col=c(rep(1,t),rep(2,t)),pch=19,main=paste(t,'samples'))
}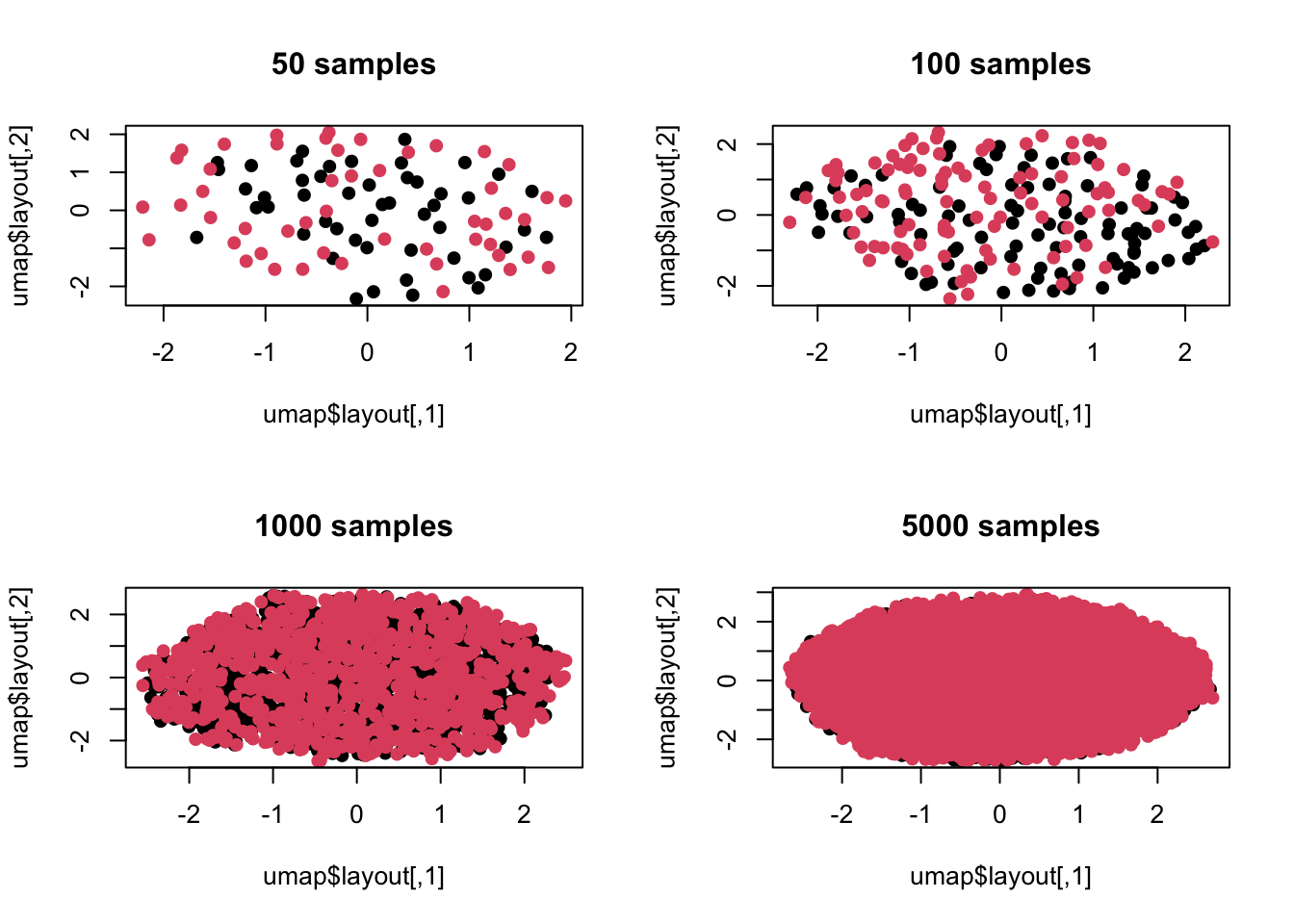
上面是用流形学习里的umap来进行的可视化,可以看出情况一致,毕竟我们模拟时差异并非是非线性的,所以流形学习也没法捕捉这种差异。
此处我想说的是,如果我们过分依赖差异分析,在大数据量背景下,大概率会检测到一些客观存在但微弱的差异,这些差异只在均值水平才能发现,具体到个体差异里很难看出来,属于统计意义可能大于实际意义的范畴。
这种情况不大可能发生在样品数小于维度数的场景下,那个场景里最大的问题是差异分析功效不足,增大样品量总是有益的。但却可以发生在维度远低于样品数,此时大数定律反而成了负面作用,因为我们总能发现差异或者说规律,但却缺少用专业知识来筛选差异实际意义的手段。
很显然,此时主成分分析或聚类分析这些方法都没啥用,这些自上而下的方法根本就看不出数据中的异质性。不过,这倒可能帮我们过滤掉哪些微弱差异,只能暂时认为这些差异就是无关紧要的。但此时会遇到的问题就是我开头说的悖论,明明差异分析发现了大量差异,但整体就好像糊成一片,如果数据分析经验不足可能就不知道咋解释了。
这种微弱的差异本质就是 type M 型错误,也就是如果效应比较弱,我们测到了也没实际意义。不仅仅是数据分析,在我们日常生活中这种错误也很常见,例如财经新闻在每天收市后的报道经常就是“受某某影响,今天大盘下降零点几个百分点”。零点几个百分点其实是属于随机过程,并不受某某影响,但即使是财经专家也要对着一堆噪音去找解释。更搞笑的是,这些专家的追随者在听了专家点拨后,马上也看到了潜在的规律性,然后带着优越感去跟其他人说你们能力不行,想不到这么远之类的。但问题是本来也没规律性啊,或者说这个所谓的规律本身的不确定性是大于确定性的。也就是当样本间方差足够大时,样本间均值差异的实际意义就很微弱了。好比两国人均GDP有显著差异,但两个国家内部贫富差异悬殊,此时与其比对人均GDP,不如把两国穷人划分成一类,富人划分成一类来进行对比,此时发现的问题可能更有实际意义。
我一般不讨论社会科学规律,很大原因在于这些学科没有完成科学化改造,其规律性更像是一种自我实现的过程。也就是我首先构建一套逻辑自洽的理论,然后用理论指导实践,怎么做怎么对,用实际行动证明理论可行性。但如果同一个学科存在两种逻辑都自洽且都经过事实检验的理论,那你很难说哪种就是客观规律,或者说不存在最优路线,这就跟科学规律不一样了。自然科学规律是相对唯一的,做不到既同意理论A又同意理论B,最后一定会被更一般性的理论C统一起来。社会科学里的很多所谓规律其实是很主观的学术观点或认知体系,好一点的可以通过观察实验来证明,极端的就单纯讲逻辑自洽,在自己理论圈子里满地打滚抱团取暖,而他们眼中的金科玉律也许就像是上面我模拟的那样,客观存在但实际没意义,或者压根分类就不合理。
要警惕那些大数据带来的发现。