因果关系能否直接从数据中获取这个问题对很多人而言答案是否定的,相关不代表因果都成了说烂了的老梗。根源上人认识世界只能通过可感知的现象,背后的规律都是在抽象意义上自洽但现实表现都含有噪音。说夸张点普朗克尺度已经界定了测量手段的极限,有些理论可能就是永远无法实证但数学上自洽的。过去的一个世纪是实验与测量技术大突破的100年,无数现代仪器或仅仅就是传感器为各类科学研究提供了大量的现象数据,也营造了数据无所不能的幻象。说是幻象是因为数据背后不仅仅有规律,也有内生的噪音,很多研究痴迷于换用不同的数据模型来提高预测性,但却忽略数据信噪比,当信噪比很低时任何结论都会不靠谱,不同模型有矛盾的预测结果无法说明模型的优劣而仅仅就是现象本身方差太大,所谓的信号或者规律其实是内生噪音的随机性导致的。
不过因果推断就是尝试解决这个问题的。最近有一个暴露组学的数据挑战,里面给出了一组人群数据,涵盖了暴露组、基因组、表观基因组、代谢组的数据,用来寻找包括哮喘在内的多种表型差异。第一眼看上去就像是系统生物学的研究,但因为有暴露组跟基因组数据,就又像是想解决一个历史性的科学问题,那就是健康究竟是基因还是外界暴露说了算。不过表观基因组跟代谢组的数据则成了这个模型的关键问题,因为这两组数据都受基因跟外界暴露的调控,而最终的结果可能就是疾病发病率。简单说就是下面这样一个模型:
外界环境 -> 暴露组 -> 表观遗传组/代谢组 -> 健康状态
遗传 -> 基因组 ->
这就是因果关系图了,因果分析有两个应用场景,一个是效应估计,就是找出各自的贡献;另一个则更关键,就是提取因果关系。像上面这个数据挑战需要解决的就是前者,因为背后的模型基本是固定的。但这里要明确这个模型逻辑上通但测量上不一定测的准,基因组也可能被环境调控,同时很多暴露影响也有遗传上的共同因素例如住在祖屋里,这就是前面说的内生噪音,因此不论是模型推断还是拟合,不确定性是一定存在的,很小的效应就是会看不出来或者不同模型给不同答案,Gelman 一直强调的 Type M 错误是科研中一定要注意的,效应太小就是实际意义不大,甚至科学上都会因为重现性差而没意义。
但其实我更好奇的是,假如没有这个模型,我们能不能从一堆数据中提炼出一个因果结构。我找来找去发现了PC算法,用来发现数据中存在的因果关系,这里记录一下。
首先,我们先仿真一组因果数据:
E <- 6*rnorm(1000,10,1)+rnorm(1000)
G <- rnorm(1000,50,2)+rnorm(1000)
M <- E*0.7+G*0.3+rnorm(1000)
Epi <- E*0.1+G*0.9+rnorm(1000)
Asthma <- 0.6*M+0.4*Epi+rnorm(1000)
data <- cbind.data.frame(E,G,M,Epi,Asthma)
cor(data)## E G M Epi Asthma
## E 1.00000 -0.02042 0.9647 0.2565 0.8551
## G -0.02042 1.00000 0.1314 0.8550 0.3549
## M 0.96474 0.13144 1.0000 0.3733 0.9159
## Epi 0.25647 0.85500 0.3733 1.0000 0.5888
## Asthma 0.85509 0.35488 0.9159 0.5888 1.0000pairs(data)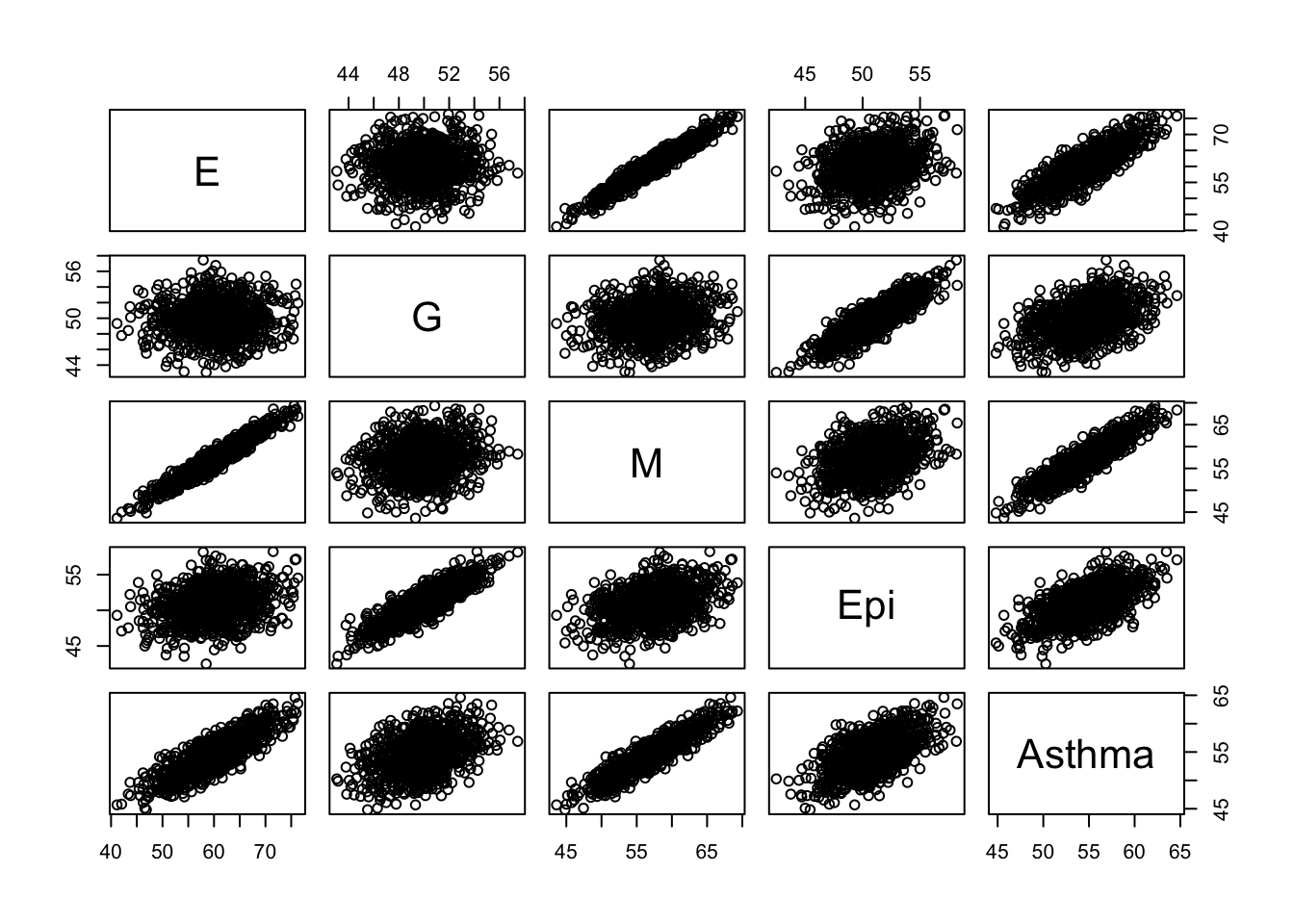
cor.test(Asthma,E)##
## Pearson's product-moment correlation
##
## data: Asthma and E
## t = 52, df = 998, p-value <2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8375 0.8709
## sample estimates:
## cor
## 0.8551cor.test(Asthma,G)##
## Pearson's product-moment correlation
##
## data: Asthma and G
## t = 12, df = 998, p-value <2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.2995 0.4079
## sample estimates:
## cor
## 0.3549这里E代表暴露组、G代表基因组、M代表代谢组、Epi代表表观组、Asthma代表疾病,仿真中设定疾病六成可以被代谢组解释而四成可以用表观组解释,然而代谢组里七成是环境影响而三成是基因影响,表观组则是一成环境影响而九成基因影响。这里我们可以看到如果进行简单回归,基本就是一团乱码。
下面我们用PC算法拟合一下试试:
library(pcalg)
suffStat <- list(C=cor(data), n = nrow(data))
pc.fit <- pc(suffStat, gaussCItest, p = ncol(data), alpha = 0.01, verbose = TRUE)## Order=0; remaining edges:20
## x= 1 y= 2 S= : pval = 0.519
## x= 1 y= 3 S= : pval = 0
## x= 1 y= 4 S= : pval = 1.2e-16
## x= 1 y= 5 S= : pval = 0
## x= 2 y= 3 S= : pval = 2.987e-05
## x= 2 y= 4 S= : pval = 0
## x= 2 y= 5 S= : pval = 1.067e-31
## x= 3 y= 1 S= : pval = 0
## x= 3 y= 2 S= : pval = 2.987e-05
## x= 3 y= 4 S= : pval = 3.173e-35
## x= 3 y= 5 S= : pval = 0
## x= 4 y= 1 S= : pval = 1.2e-16
## x= 4 y= 2 S= : pval = 0
## x= 4 y= 3 S= : pval = 3.173e-35
## x= 4 y= 5 S= : pval = 4.855e-101
## x= 5 y= 1 S= : pval = 0
## x= 5 y= 2 S= : pval = 1.067e-31
## x= 5 y= 3 S= : pval = 0
## x= 5 y= 4 S= : pval = 4.855e-101
## Order=1; remaining edges:18
## x= 1 y= 3 S= 4 : pval = 0
## x= 1 y= 3 S= 5 : pval = 0
## x= 1 y= 4 S= 3 : pval = 2.175e-46
## x= 1 y= 4 S= 5 : pval = 3.191e-101
## x= 1 y= 5 S= 3 : pval = 2.84e-18
## x= 1 y= 5 S= 4 : pval = 0
## x= 2 y= 3 S= 4 : pval = 1.207e-38
## x= 2 y= 3 S= 5 : pval = 1.84e-72
## x= 2 y= 4 S= 3 : pval = 0
## x= 2 y= 4 S= 5 : pval = 0
## x= 2 y= 5 S= 3 : pval = 4.245e-101
## x= 2 y= 5 S= 4 : pval = 1.425e-31
## x= 3 y= 1 S= 2 : pval = 0
## x= 3 y= 1 S= 4 : pval = 0
## x= 3 y= 1 S= 5 : pval = 0
## x= 3 y= 2 S= 1 : pval = 1.174e-94
## x= 3 y= 2 S= 4 : pval = 1.207e-38
## x= 3 y= 2 S= 5 : pval = 1.84e-72
## x= 3 y= 4 S= 1 : pval = 1.184e-65
## x= 3 y= 4 S= 2 : pval = 1.006e-69
## x= 3 y= 4 S= 5 : pval = 4.762e-71
## x= 3 y= 5 S= 1 : pval = 5.469e-142
## x= 3 y= 5 S= 2 : pval = 0
## x= 3 y= 5 S= 4 : pval = 0
## x= 4 y= 1 S= 2 : pval = 8.164e-77
## x= 4 y= 1 S= 3 : pval = 2.175e-46
## x= 4 y= 1 S= 5 : pval = 3.191e-101
## x= 4 y= 2 S= 1 : pval = 0
## x= 4 y= 2 S= 3 : pval = 0
## x= 4 y= 2 S= 5 : pval = 0
## x= 4 y= 3 S= 1 : pval = 1.184e-65
## x= 4 y= 3 S= 2 : pval = 1.006e-69
## x= 4 y= 3 S= 5 : pval = 4.762e-71
## x= 4 y= 5 S= 1 : pval = 2.8e-195
## x= 4 y= 5 S= 2 : pval = 7.757e-101
## x= 4 y= 5 S= 3 : pval = 5.666e-140
## x= 5 y= 1 S= 2 : pval = 0
## x= 5 y= 1 S= 3 : pval = 2.84e-18
## x= 5 y= 1 S= 4 : pval = 0
## x= 5 y= 2 S= 1 : pval = 4.455e-179
## x= 5 y= 2 S= 3 : pval = 4.245e-101
## x= 5 y= 2 S= 4 : pval = 1.425e-31
## x= 5 y= 3 S= 1 : pval = 5.469e-142
## x= 5 y= 3 S= 2 : pval = 0
## x= 5 y= 3 S= 4 : pval = 0
## x= 5 y= 4 S= 1 : pval = 2.8e-195
## x= 5 y= 4 S= 2 : pval = 7.757e-101
## x= 5 y= 4 S= 3 : pval = 5.666e-140
## Order=2; remaining edges:18
## x= 1 y= 3 S= 4 5 : pval = 2.984e-295
## x= 1 y= 4 S= 3 5 : pval = 3.844e-29
## x= 1 y= 5 S= 3 4 : pval = 0.577
## x= 2 y= 3 S= 4 5 : pval = 2.05e-08
## x= 2 y= 4 S= 3 5 : pval = 4.093e-267
## x= 2 y= 5 S= 3 4 : pval = 0.4735
## x= 3 y= 1 S= 2 4 : pval = 0
## x= 3 y= 1 S= 2 5 : pval = 4.25e-304
## x= 3 y= 1 S= 4 5 : pval = 2.984e-295
## x= 3 y= 2 S= 1 4 : pval = 1.062e-28
## x= 3 y= 2 S= 1 5 : pval = 3.746e-09
## x= 3 y= 2 S= 4 5 : pval = 2.05e-08
## x= 3 y= 4 S= 1 2 : pval = 0.1595
## x= 3 y= 5 S= 1 2 : pval = 1.519e-51
## x= 3 y= 5 S= 1 4 : pval = 1.218e-71
## x= 3 y= 5 S= 2 4 : pval = 0
## x= 4 y= 1 S= 2 3 : pval = 1.981e-08
## x= 4 y= 1 S= 2 5 : pval = 0.1367
## x= 4 y= 2 S= 1 3 : pval = 0
## x= 4 y= 2 S= 1 5 : pval = 3.064e-224
## x= 4 y= 2 S= 3 5 : pval = 4.093e-267
## x= 4 y= 5 S= 1 2 : pval = 7.358e-24
## x= 4 y= 5 S= 1 3 : pval = 1.651e-120
## x= 4 y= 5 S= 2 3 : pval = 7.409e-36
## x= 5 y= 3 S= 1 2 : pval = 1.519e-51
## x= 5 y= 3 S= 1 4 : pval = 1.218e-71
## x= 5 y= 3 S= 2 4 : pval = 0
## x= 5 y= 4 S= 1 2 : pval = 7.358e-24
## x= 5 y= 4 S= 1 3 : pval = 1.651e-120
## x= 5 y= 4 S= 2 3 : pval = 7.409e-36
## Order=3; remaining edges:10plot(pc.fit,main='Demo',labels=c("E","G","M","Epi","Asthma"))## Loading required namespace: Rgraphviz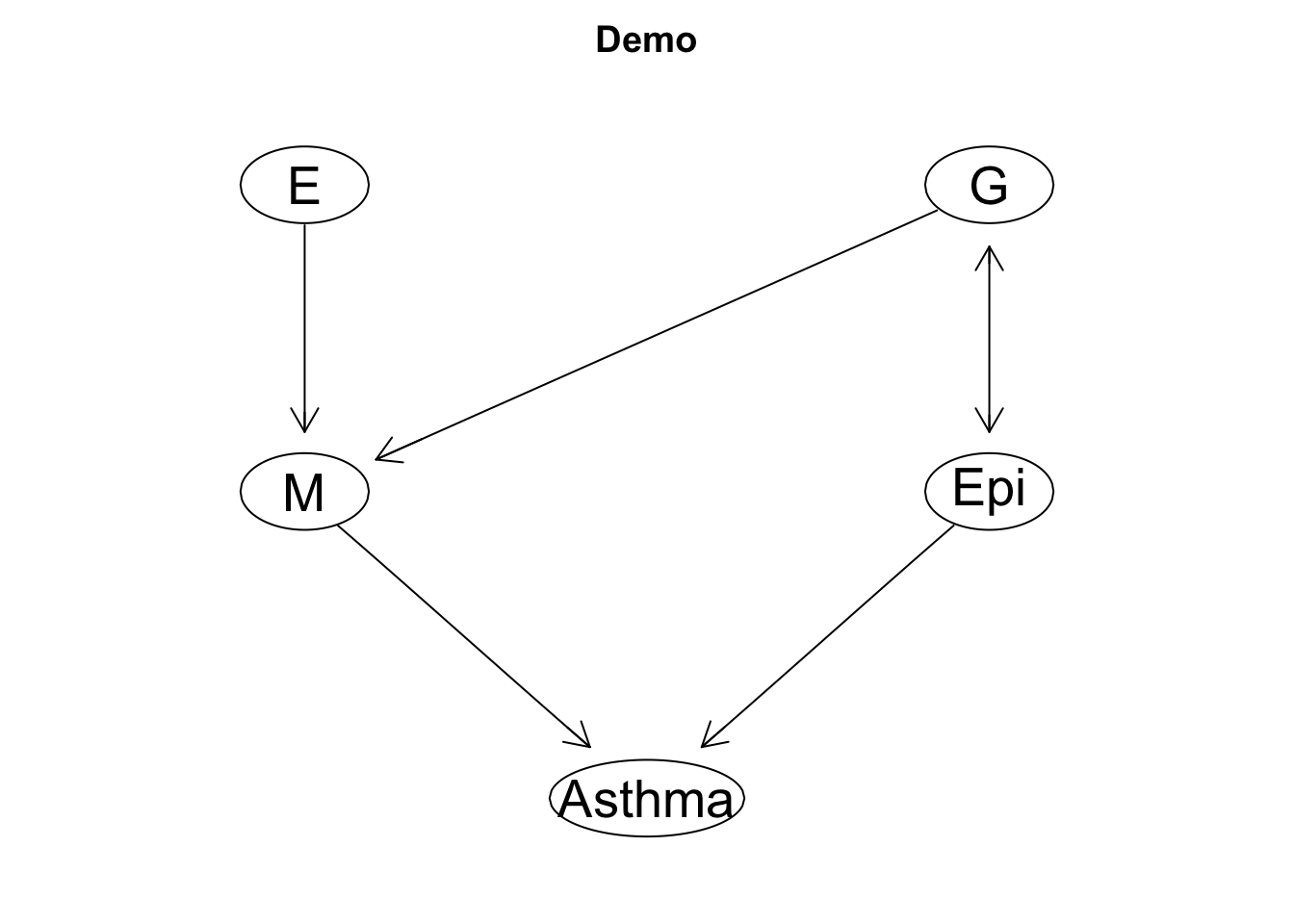
怎么说呢,结果还算满意,虽然细节上还有点问题(例如E跟Epi间效应比较弱就没被算法发现),基本符合我们仿真的设定,这也算是一种内生噪音的后果吧,就算是仿真也可能搞出随机相关来。
现在我们来说下PC算法究竟啥原理。本质上PC算法一直在反复做条件独立性假设检验,这里我们指定的就是 Gaussian 检验,算的其实就是多变量间的偏相关性然后通过假设检验决定连接。至于方向性,越是结果其内生噪音应该越大。
不过这种直接依赖数据的因果结构发现适用范围非常有限,前面这个例子我用了线性模拟与检验才会有个说得过去的结果,要是本来不是这种分布,结果意义就不大了。什么?你问真实数据?,真实数据E跟G加起来上万维,M跟Epi的维度也是这个量级,信噪比不高的话根本啥都找不出来,找出来的因果结构说不定还是Epi在G上面,所以我一直以来就认为组学数据分析的出路在于提高信噪比而不是盲目往里送维度。但降维就要丢信息,如何权衡有效信息量很重要,而这个有效的判定则是根据实际问题来,不同问题的降维策略应该是不一样的,这就需要研究人员根据实际情况决策了。
科学问题不等同因果问题或相关问题,因果律也只是研究工具的一种,噪音才是科学求证的公敌。