诺谟图(Nomography),又称列线图解法,于1884年由Philbert Maurice d’Ocagne (1862-1938)发明来用图形化计算解决复杂函数的求值方法。随着计算机数值计算的发展逐渐淡出人们的视线,但有必要将其拎出来重新讨论一下。一方面是重新演绎直观计算过程有助于消除科学的神秘性并增加趣味性,另一方面则是我个人的一种直觉:诺谟图似乎要在科学的某些领域复活并展示其巨大的威力,此外诺谟图的设计本身就是一种艺术创作,甚至同一个方程会出现两种完全不同的设计方式。这里我先大概翻译转述下Ron Doerfler 写的一篇论文里我能看懂的部分来讲下原理,然后扩展讨论下历史,最后讲下其在当前统计学里的应用。
原理篇

最简单的诺谟图是上面的摄氏度与华氏度的转化图,其本质也是一个计算尺,其区别在于计算尺可通过多步计算来实现更多种类的方程计算而诺谟图则侧重于一步解决一个特殊的方程。其实诺谟图的一般形式是通过将含三个或三个以上的变量的方程中的变量用标尺表示,然后通过等值线(isopleth)将所有已知变量连接,这样未知的变量也就知道了。当然不同变量的标尺的位置是通过前期设计得到的,而这种表示方式要比3D图更为直观也易于接受。
平行线式诺谟图是最简单也是最经典的一种多变量诺谟图,其基本形式与图式如下:
$$f_1(u) + f_2(v) = f_3(w)$$
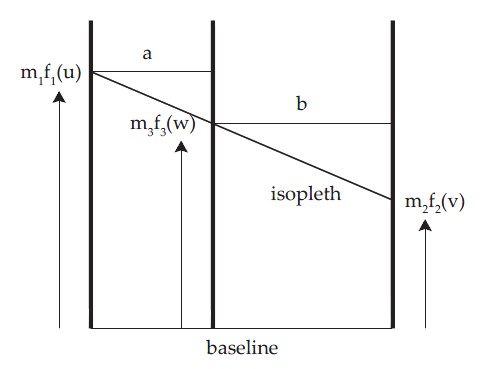
其中,$m_1$,$m_2$,$m_3$代表的是比例因子,在一条等值线穿过这三条平行线后,根据相似三角形原理我们可以建立如下方程:
$$\frac{m_1f_1(u)-m_3f_3(w)}{a} = \frac{m_3f_3(w) - m_2f_2(v)}{b}$$
整理后可得:
$$m_1f_1(u) + \frac{a}{b} m_2f_2(v) = (1+ \frac{a}{b})m_3f_3(w)$$
对照最初的基本形式,我们要做的就是消去与$m$、$a$、$b$相关的部分,如下:
$$m_1 = \frac{a}{b}m_2 = (1+ \frac{a}{b})m_3$$
整理可得到下面的公式:
$$\frac{m_1}{m_2}=\frac{a}{b}$$
$$m_3 = \frac{m_1*m_2}{m_1+m_2}$$
好了,我们现在知道了比例因子的关系,同时我们也知道想要画的图的大小与我们关心的变量变动范围,而根据已知变量$f_1(u)$与$f_2(v)$的变动范围与图的高度我们可以确定 $m_1$、$m_2$与$m_3$,根据 $m$的取值与图的宽度可以定出直线 $f_3(w)$的位置,这样由于在图上$f_1(u)$、$f_2(v)$与$f_3(w)$的坐标都是线性均匀分布的,现在就可以用等值线来进行求解了。
也许看到这里你会说求个线性方程费这么大的劲是没意义的,但线性方程可不仅仅就这一种形式,原则上可以转化为线性方程的方程都可以用诺谟图来求解,例如下面的两种转化
$$log(cd) = log c + log d$$
$$log(c^d) = d log c$$
其实,这样做的同时你也会发现标尺不再是均匀的了,但没关系,因为我们在绘图时依然可以采用均匀的标尺,然后附加一个对数表就够了,要是有耐心可以把标尺按原始数据绘制上去,这都不影响我们计算的准确性。
上面的理论分析太过枯燥,下面我们用一个例子来展示在处理复杂的工程经验方程时诺谟图的绘制。方程如下:
$$(1.2*D + 0.47)^{0.68}*(0.91T)^{3/2} = N$$
我们关心的范围是$1.0<D<8.0$与$1.0<v<2.0$,而$u$与$v$的长度都设置为11cm而宽度设置为6cm,首先进行方程变形:
$$0.68 log(1.2D + 0.47) + 1.5 log T = logN − 1.5 log 0.91$$
然后根据图形长度范围与参数范围求解 $m$:
$$m_1 =\frac{11}{0.68 log(1.2(8.0) + 0.47) − 0.68 log(1.2(1.0) + 0.47)}= 20.73$$
$$m_2 =\frac{11}{1.5 log 2.0 − 1.5 log 1.0}= 24.36$$
$$m_3 = \frac{m_1*m_2}{m_1 +m_2}= 11.20$$
根据宽度范围求解第三条线的位置
$$\frac{a}{b}= \frac{m_1}{m_2}= 0.851$$
$$a + b = 6$$
$$b = 3.241 cm, a = 2.759 cm$$
好了,我们开始画图。
在D轴上我们的起始点是1.0,然后按照下面的公式在11cm的范围中求坐标
$$20.73 *(0.68 log(1.2D + 0.47) − 0.68 log(1.2(1.0) + 0.47))$$
然后画$T$的范围,起始点依旧是1.0。坐标公式如下:
$$24.36(1.5 log T − 1.5 log 1.0)$$
最后我们距离D轴2.759cm处垂直基线画一条N轴,起始点通过下面公式求出:
$$(1.2(1.0) + 0.47)^{0.68}*(0.91(1.0))^{1.5} = 1.230$$
坐标通过下面公式求出:
$$11.20*(logN − 1.5 log(0.91))$$
OK,现在我们可以得到这张诺谟图了。使用的时候我们只需要知道任意两轴上的数做延长或相交,就可以知道第三轴的数了。这个过程完全依赖直尺比划就可以,类似于查表(不知道现在还教不教)。我们可以看出诺谟图在求解复杂方程上是很方便的,甚至可以求解一些无解析解的方程。
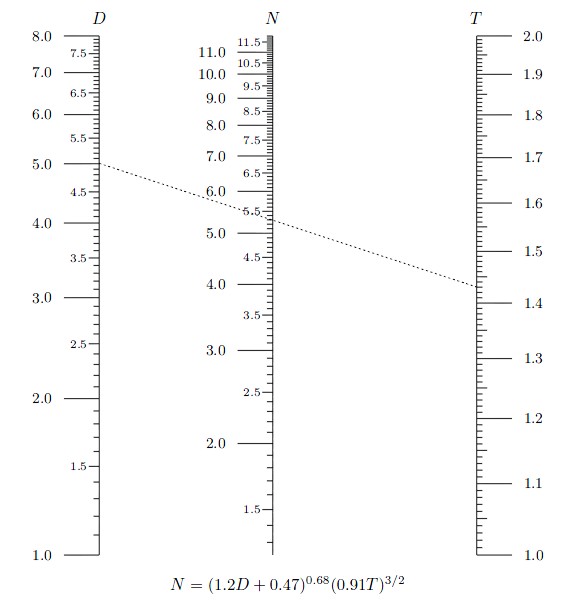
除了平行线型图,N型图可以用来解决带有除法的公式:
$$f_3(w) = \frac{f_1(u)}{f_2(v)}$$
例如这种求圆柱体积的图:
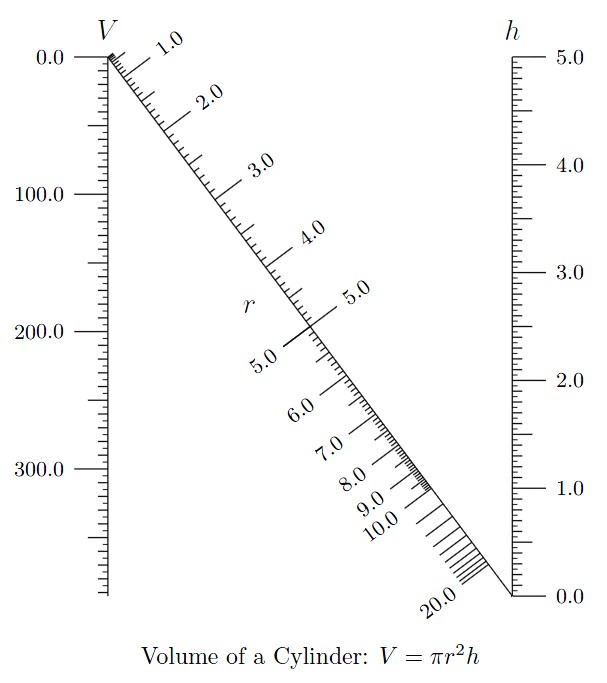
还有涉及四个变量的比例图,原理也是相似三角形。例如下面这种理想气体公式,你需要画两条线,先连接已知的两个变量,此时与中间对角线有个交点,然后连接交点与另一个已知变量并延长,就知道剩下的那一个变量是什么了。
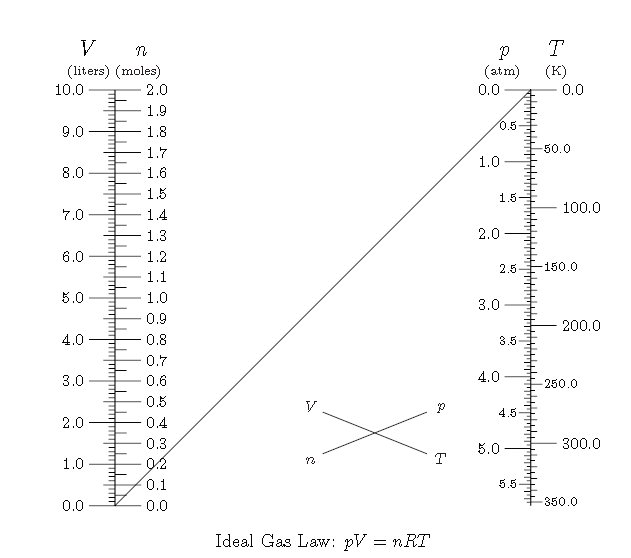
类似的还有正弦定理:
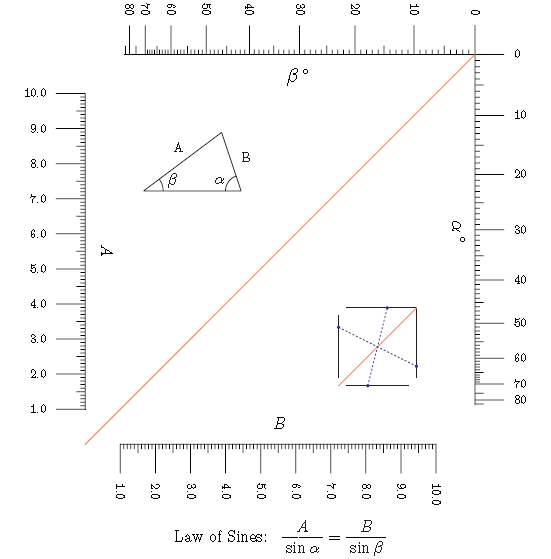
利用相似三角形的性质,如平行、垂直、 还可以得到下面的图形:
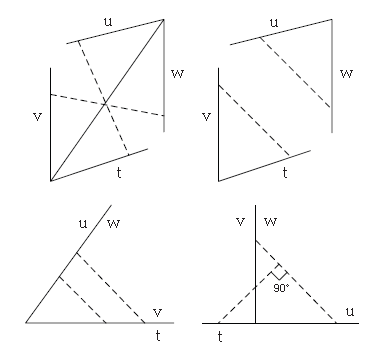
还有一种图的原理是依赖等腰三角形的,用来解决并联电阻求值问题。
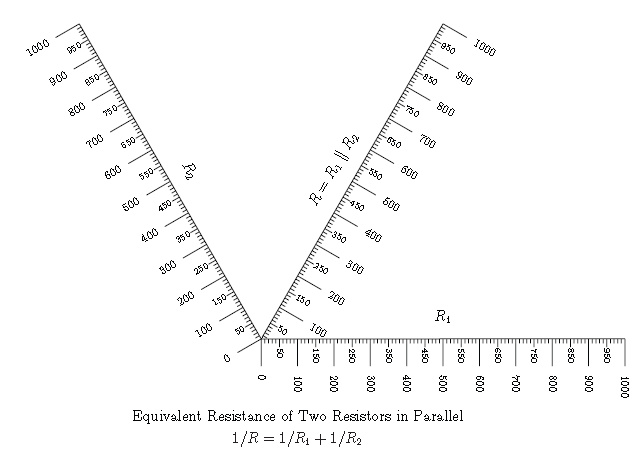
当然,你也可以将多种图组合求解一个复杂但可拆分的方程。但更本质的方法则是把所有的比例关系都转成行列式结构,通过网格还可以绘制更为复杂但直观的诺谟图,方便工程应用,也有一定的艺术价值。原理请直接读论文。
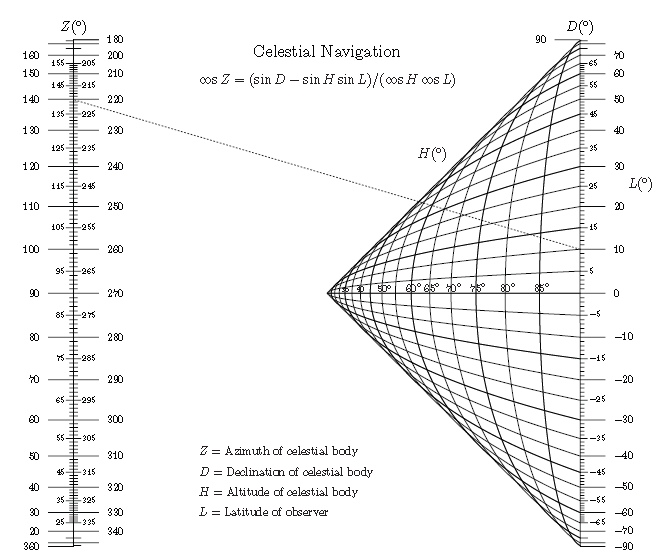
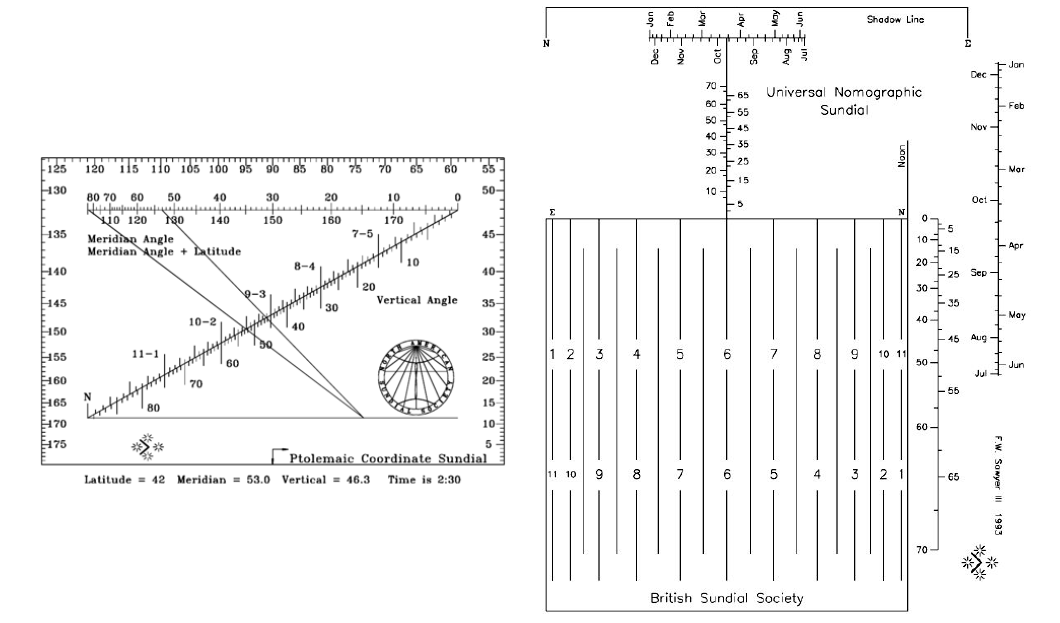
通过对原始变量的转换,例如平移、旋转、剪切、拉伸、投影, 基本上可以把诺谟图应用到各个数值求解的过程中去。 而实际需求的数值范围则是设计图表中最重要的因素,通过一定的转换会让诺谟图更像是一件艺术品。其实日晷就是一个诺谟图应用的很好实例。这里放个Ron Doerfler自己设计的日晷图。
历史篇
说了这么多你可能会好奇,这个东西是怎么出现的?其实我们可以扯的远一些,聊下图(graph)是怎么出现的。也许很多人没意识到,直到1878年,“graph”这个词才被数学家引入到研究中,用来表示化学-代数关系,而在这之前,图更多使用在天文与地理研究之中,例如天象图与地图。值得注意的是历史中图并不是抽象表达而更多是对真实事物的描述,当然几何求解数值方程的方法也算是历史悠久了。古人用的星盘与四分仪就是基于这种方法设计的,这对宗教的传播与未知世界的探索提供了可靠的保障,但这些更多是测量方法,需要借助实物与观察。
研究中用的图,特别是带有笛卡尔坐标系来展示真实数据的图其实出现的并不早。根据《Blood, Dirt, and Nomograms: A Particular History of Graphs》的记载,最早的图可以追溯到1770年左右,而且有三个起源。第一个起源是英国人 William Playfire 做统计图集时作的图,用来描述英国国债。
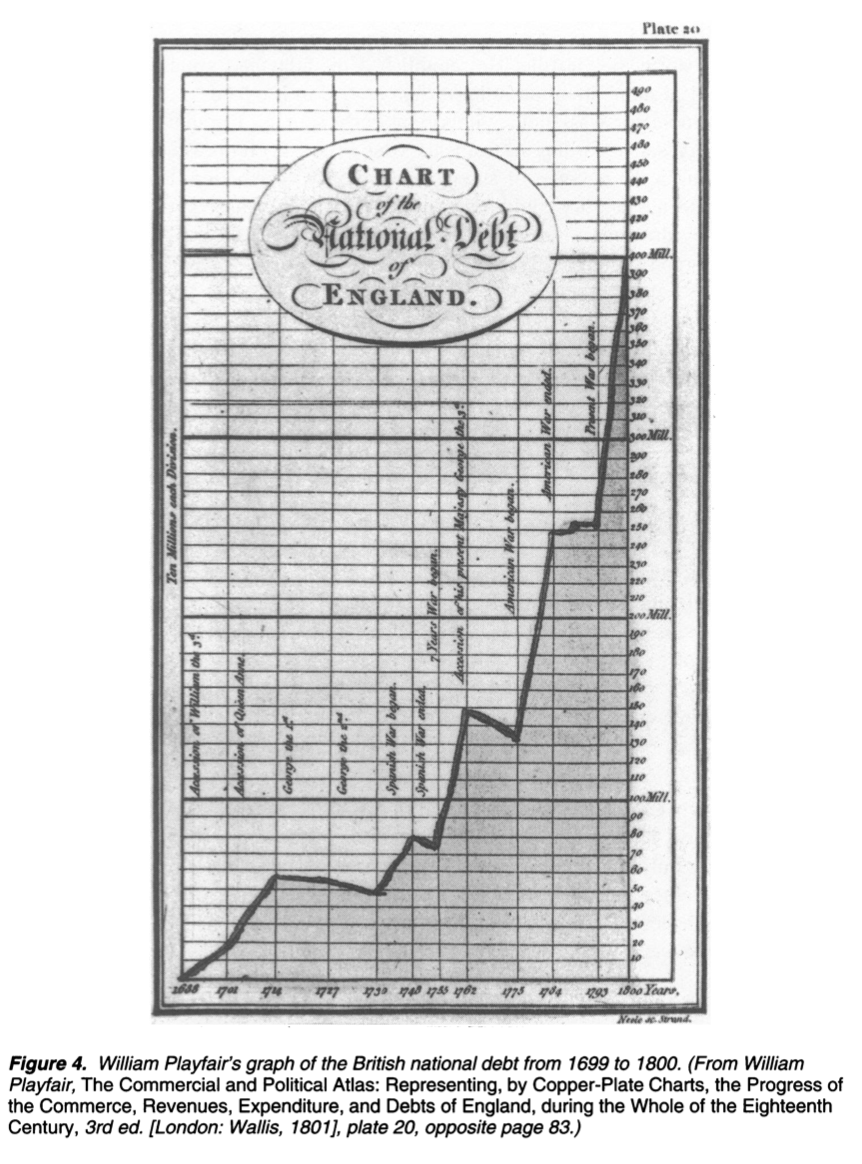
第二个起源是 James Watts 搞的,用来绘制引擎的压力体积变化,这个图就不是人画的了,直接就是机器画。在那个年代其实计数对于机械过程是个麻烦事,所以就直接给机器接上个机械臂,其变动用机械臂的震动记录在纸上。这种物理信号直接输出的仿真信号图后来广泛应用在地震监测、心率监测等领域,当然会有坐标系来校准。
第三个起源是 Johann Heinrich Lambert 的实验记录,此君是科学家出身,坚持自然哲学要用观察数据来量化测量,在这个过程中他制作了大量的图。这里要说明的是自然哲学是相对于博物学来说的,那个年代自然哲学侧重今天的物理学研究关注形而上的东西与分析手段而博物学侧重对自然的宏观观察记录,侧重经验感知与综合。国内经常说的科普其实很多是在博物学这个层面上的,例如逛博物馆,野外考察什么的,侧重知识性。博物学很重要但其实国内缺的是自然哲学这块的思维普及而不仅仅是一个个知识点。
然而,这个概念搞出来后在四十年里几乎没有人关注,原因在于懂这个技术的人还不知道咋用或者需要用的人不知道有这个技术。1795年法国大革命后引入了计量系统,在对公众推广时发现公众对数字无感,这时有个叫 Pounchet 的棉花制造商发现了 William Playfire 的图,他觉得这个图很有前景。其做的第一个应用就是把乘法表给图表化了。
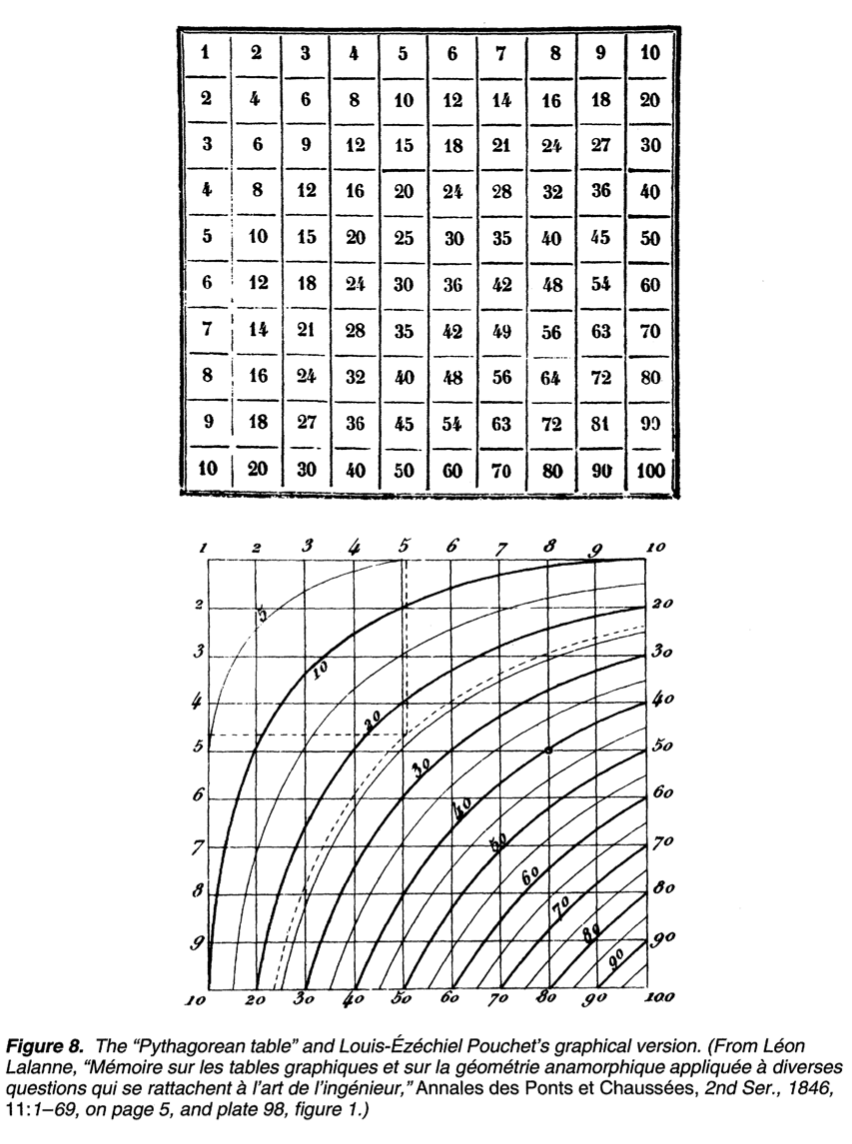
这个图咋用呢,打比方我想知道6乘7的结果,我就沿着6的横网格找7的竖网格,里面的等值线就可以告诉我乘积在40到50之间,这对于不懂算术的人应该是非常方便了。但他其实已经将原始但两个变量关系图推广到了三变量关系了。在另一方面,法国的工程师们开始关注投影几何对于堡垒建设的应用,例如堡垒需要修建多么高?怎样最快运送沙土?其后继者接触了 Pounchet 的图后突然发现,投影几何其实可以用在这种存在等值线的图之中。
所谓投影几何,就是将一组几何关系投影到另一个自定义的坐标系里的几何方法,说白了就是坐标变化。投影几何里的经典作品就是下面这个描述拿破仑大撤退的图,在图形可视化领域里也是经典作品。
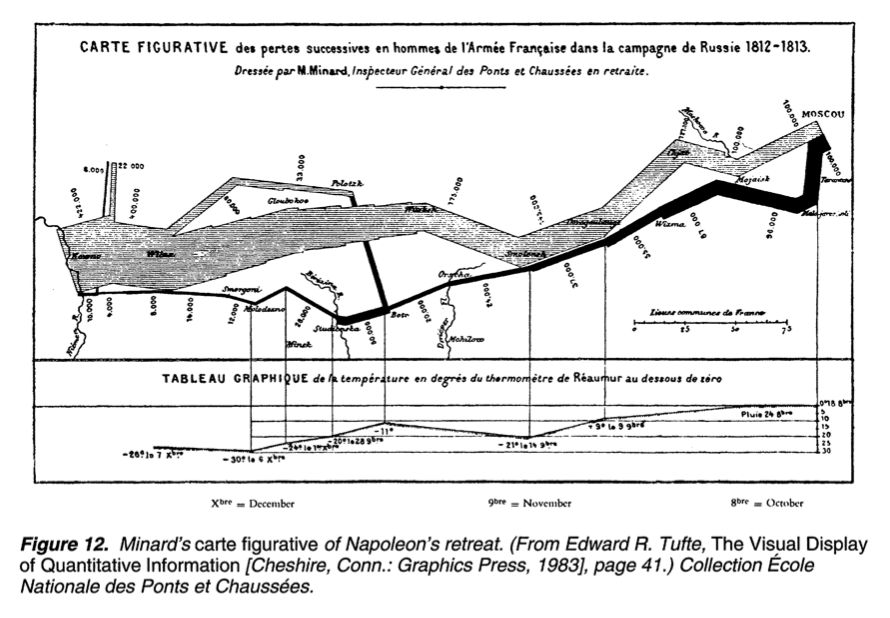
有位叫 Lalanne 的法国工程师将 Pounchet 的这种图示方法广泛推广到工程领域,特别是他把等值线跟地图结合,就有了我们现在看到的等值线地形图,这样三维数据就可以二维展示了。其第二个贡献就在于对数坐标轴的引入,从绘图角度,曲线不如直线好画,他发现把数据对数化后曲线可以变直线,这就是投影几何的一种映射。此时,图已经有了计算属性了。
到了1884年,Philbert Maurice d’Ocagne 进一步将图形计算与投影几何结合,这就有了我们前面看到的诺谟图。而诺谟图事实上通过等值线超越了笛卡尔坐标系,多个参数可以几何投影到多条线但保证其函数关系可以被等值线来描述,使用起来也非常方便,完全不需要学习几何学与函数理论,会划线就可以。在第一次世界大战中,几乎每个防空炮兵都有一个诺谟图,根据当时情况来计算开炮的方位与角度。
如果你认为诺谟图就是工程上可以用就错了,诺谟图其实在生理学里曾经有统治地位。20世纪初,生理学研究人员意识到人体血液是一个及其复杂的系统,里面有各种各样的化合物,其浓度其实存在一个平衡范围,然而将这个系统展示出来就成了大问题,如果两两关系进行绘图,那么其实超过一百幅图。此时,诺谟图闪亮登场。下面就是一副1928年哈佛生理学家 L.J.Henderson 在耶鲁大学作报告时用的图,他认为这张图浓缩了当时人类对血液的所有知识。
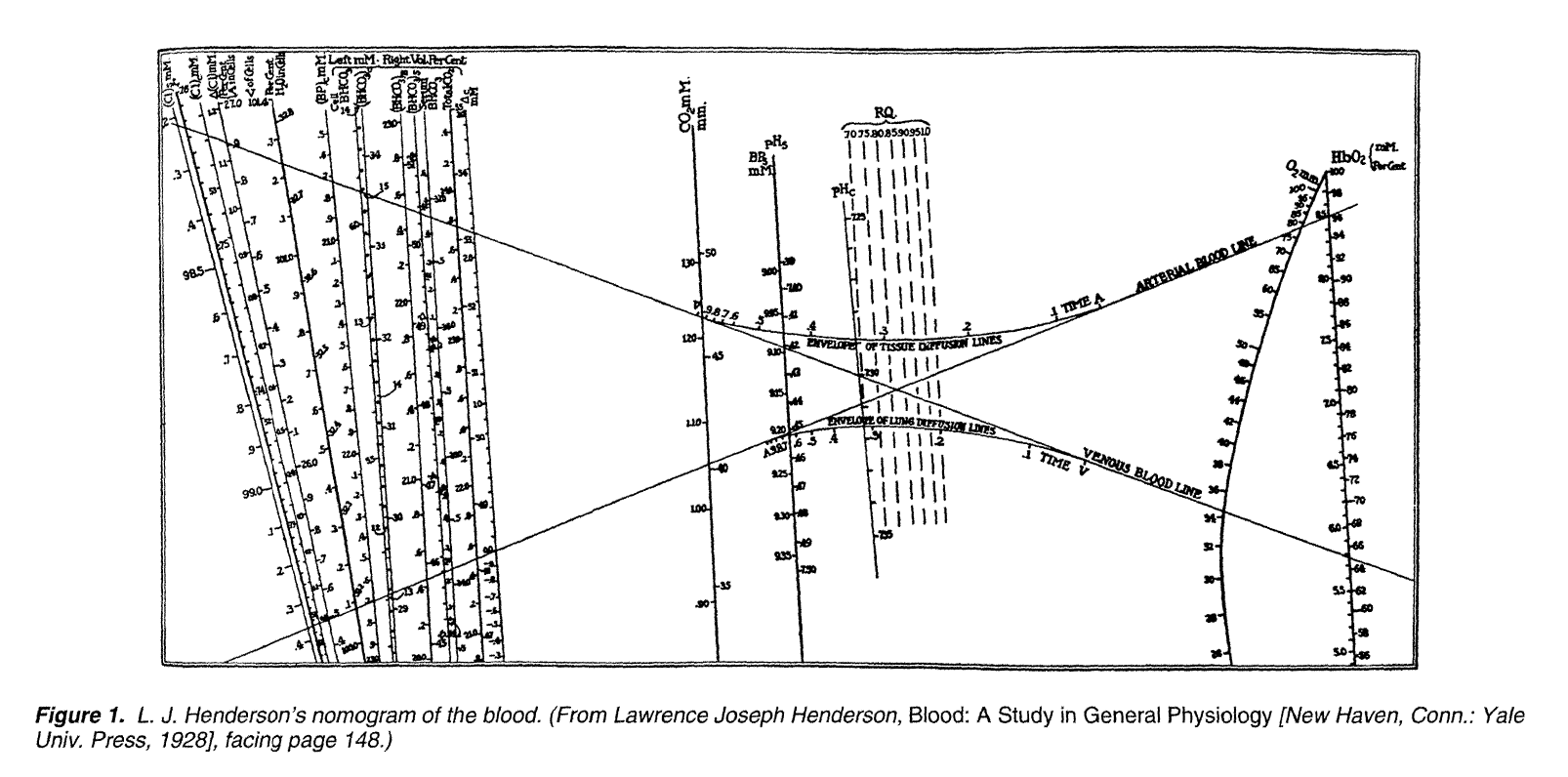
确实,诺谟图在浓缩知识上可能是个顶峰,如果我们打算给后人留一些证明文明存在的证据,也许这样一张图比复杂的公式要更实用,也更直观。哲学家 F.S.C.Northrop 认为一个多组分复杂系统可以也只可以用诺谟图来描述其动力学过程。
然而,时过境迁,今天连知道诺谟图的人都不多了,实验学科已经意识到单变量控制实验与现实的距离,然而多变量的系统或者时髦一点的组学,其实都已经不知道诺谟图这类描述系统的方法了。同当年的机器类似,或许在数据量充盈的今天,我们可以先画出图,然后反推背后的函数,甚至图本身就是解。有没有很眼熟?
回归篇
现在还有没有诺谟图,答案是肯定的,且如我前面所说,有些模型确实可以可视化为诺谟图,且所有机器学习里的黑箱模型应该都可以可视化为诺谟图且可以以图片形式保存与传递。在统计学里,有一种数据展示方法叫做回归诺谟图。例如下面这一张:
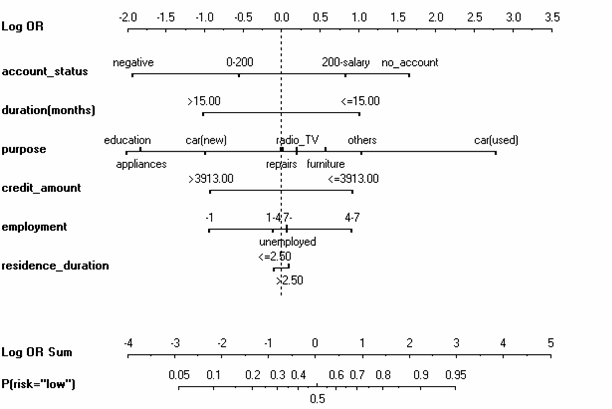
这张图的用法跟之前说的有点区别,使用的是垂直等值线,也就是说,图里六个变量你根据实际取值画一条垂直线到最上面那条 Log OR 的轴上,然后你会得到六个值,将这六个值的和计算出来算一个坐标,然后在图上画一条垂直线到下面的风险概率里,然后你就知道总体风险了。这个方法非常直观表示了不同变量取值范围及其对风险值的贡献,比单纯放个系数表上去要直观很多,但我估计在目前大学教育对诺谟图的缺失大背景下,能看懂的人估计不多,这个活原理上非常技术但其实不难。我个人曾经见到审稿人因为看不懂图就说图太复杂不如用表的情况,这种智力倒退在专业细化的今天从来没少过,甚至更多了,有些人自己脑子处理不了信息量大的图就去要信息量少但不准确的图,掩耳盗铃。其实很多复杂些的模型例如支持向量机也可以用诺谟图来展示最终结果。至于能不能做到数据直接生成,我认为并不困难,甚至比数值求解还要简单。
当然,这个活不需要你自己做。在 CRAN 上,你可以用 hdnom 包来对多变量生存分析进行诺谟图绘制。而 nomogramEx 包可用来从诺谟图图片中反向提取方程。不过我看到诺谟图的使用还是线性模型居多,应用也是更多在生存分析方面,以后应该有更多的应用方向与场景。当然,诺谟图设计本身就是个技术与艺术的结合体,如果你想修身养性平复焦虑又不愿意搞那些练字画画织毛衣的事,或许你该拿起笔来,用现在天天更新的一些数据自己设计一张诺谟图,记录下当前的大流行。
扩展阅读资料