曾经有个笑话吐槽物理学家研究鸡不下蛋问题时首先假设了一只存在真空中的球形鸡,进而认为理工类研究过于简化了现实世界,再进而推导出了一种不修边幅、不谙人情世故且高智商低情商的理工科书呆子刻板印象。就我个人生活经验而言,这种看法倒也没啥问题,对,就是没啥问题,你没看错。
但是(说“但是”前的都是废话–马克·于瘟),当今学术研究的一个大趋势就是用理工科的思维研究社会自发行为,我曾经尝试用马尔可夫过程解释社会阶层流动,但其实很多理工科出身的科学家是很严肃地研究这类问题的。我们将会看到一个松散假设下的物理模型是可以解释很多(但绝不是全部)自发的宏观社会行为的。在某些视角下,我们也许就是个真空中的球状社会信息综合体。首先,我们从具象到抽象,来了解下一个统计物理学的概念——玻尔兹曼分布。在后续的文章中我们会用这个分布来探索下社会行为,特别是经济行为。
社会行为的抽象
社会行为其实就是个体间的相互作用,在物理学视角下,这个个体间相互作用有四种(但我知道多数人不关心这个),简单说就是物质能量交换。而社会经济行为视角下,这个相互作用可以看成价值流动,通俗一点就是钱。钱可以在流通成本很低的现代信息社会下快速在社会个体间转移,在物理学视角下可看作能量在不同粒子间的传递。那么类比一下我们会发现,如果我想知道一个社会整体的财富分配,我们可以类比到一个装满带有能量的小球的空间去观察小球的能量分布。这里有:
- 社会个体(人、公司、团体)-> 空间里的小球
- 财富(钱、资产) -> 能量
- 价值交换(买卖行为、资本流动)-> 小球间能量交换
- 社会个体的财富分配 -> 空间里的能量分布
这里我们需要一些假设,首先我们考虑的是一个热力学平衡,也就是说,空间里能量总和一定,也就是要是个封闭空间,同样,社会里总财富在某个时间点也是稳定的。其次,我们想知道的是财富分布或能量分布,那么我们就要有不同财富区间与能量区间来构成分布,这里我们用钱数或能量值来划分,拥有钱数或能量在同一区间的社会个体或小球在分布中是一样的,无法区分,也是等概率的。最后,能量交换或价值交换要达到热力学平衡,这个在小球模型里很容易实现,但社会实际状态只能近似认为达到,这意味着交易是随机的且充分的,后续我们会修改这个限制让模型更符合社会实际。
根据上面的类比与假设,目前我们大概可以用一堆小球去模拟一些稳态社会行为了,这个抽象过程是大多数理工类科学研究的起点,不然一上来就过于复杂很难讨论。
封闭空间里的赋能小球
好了,目前我们先不去想复杂的社会行为来考虑小球。在一个封闭空间里,小球的能量总和是固定的,但能量范围却可以很广,小球数也可以很多,那么我们再简化下,就考虑3个球总能量6,能量区间就会有7个离散数值:0,1,2,3,4,5,6,7。那么我们想得到的是宏观状态下能量分布,我们首先来个原始方法:数。
首先要数下有多少个宏观态。例如有一个球上有6的能量,其余的球能量都只能是0。我们可以列出下面的7种宏观态:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Macrostate1 | 2 | 0 | 0 | 0 | 0 | 0 | 1 |
| Macrostate2 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| Macrostate3 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| Macrostate4 | 1 | 0 | 0 | 2 | 0 | 0 | 0 |
| Macrostate5 | 0 | 2 | 0 | 0 | 1 | 0 | 0 |
| Macrostate6 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Macrostate7 | 0 | 0 | 3 | 0 | 0 | 0 | 0 |
然后我们考虑每一种宏观态下有多少种微观态,因为球有3个,区间有7个,我们可以看成一个排列组合问题。微观下,一共有\(3!\)种排列组合,但在基本假设中,我们认为属于同一宏观状态的球是一种,那么这些情况就要被排除掉。例如在宏观态7中,虽然球可以有6种排列,但因为都在1个能量区间,实际只有1种微观态。也就是说,如果我们有N个球,排列组合上看虽然有\(N!\)种组合,但实际由于N个球中有n个球在区间i,我们要从总的排列组合中除掉这种组合。也就是:
\[ \# microstates = \frac{N!}{n_0!n_1!...n_i!} \]
这样我们可以得到共计28种微观态,在这里所有微观态的出现概率是一样的:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | Microstate | |
|---|---|---|---|---|---|---|---|---|
| Macrostate1 | 2.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 3 |
| Macrostate2 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 6 |
| Macrostate3 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 0.00 | 6 |
| Macrostate4 | 1.00 | 0.00 | 0.00 | 2.00 | 0.00 | 0.00 | 0.00 | 3 |
| Macrostate5 | 0.00 | 2.00 | 0.00 | 0.00 | 1.00 | 0.00 | 0.00 | 3 |
| Macrostate6 | 0.00 | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 6 |
| Macrostate7 | 0.00 | 0.00 | 3.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1 |
| total | 0.75 | 0.64 | 0.54 | 0.43 | 0.32 | 0.21 | 0.07 | 28 |
在宏观态1中所有微观态出现的可能性为\(3/28\),其中针对能量为0的区间贡献\(2*3/28 = 0.214\) 个小球,而宏观态2中对能量为0的也贡献\(0.214\)个小球,同样宏观态3中贡献为\(0.214\)个小球而宏观态4中贡献为\(0.107\)个小球,这样会有\(0.75\)个小球贡献给能量为0的区间,同样我们可以得到其他能量区间上有多少小球。这个小球的能量分布就是我们打算求的。
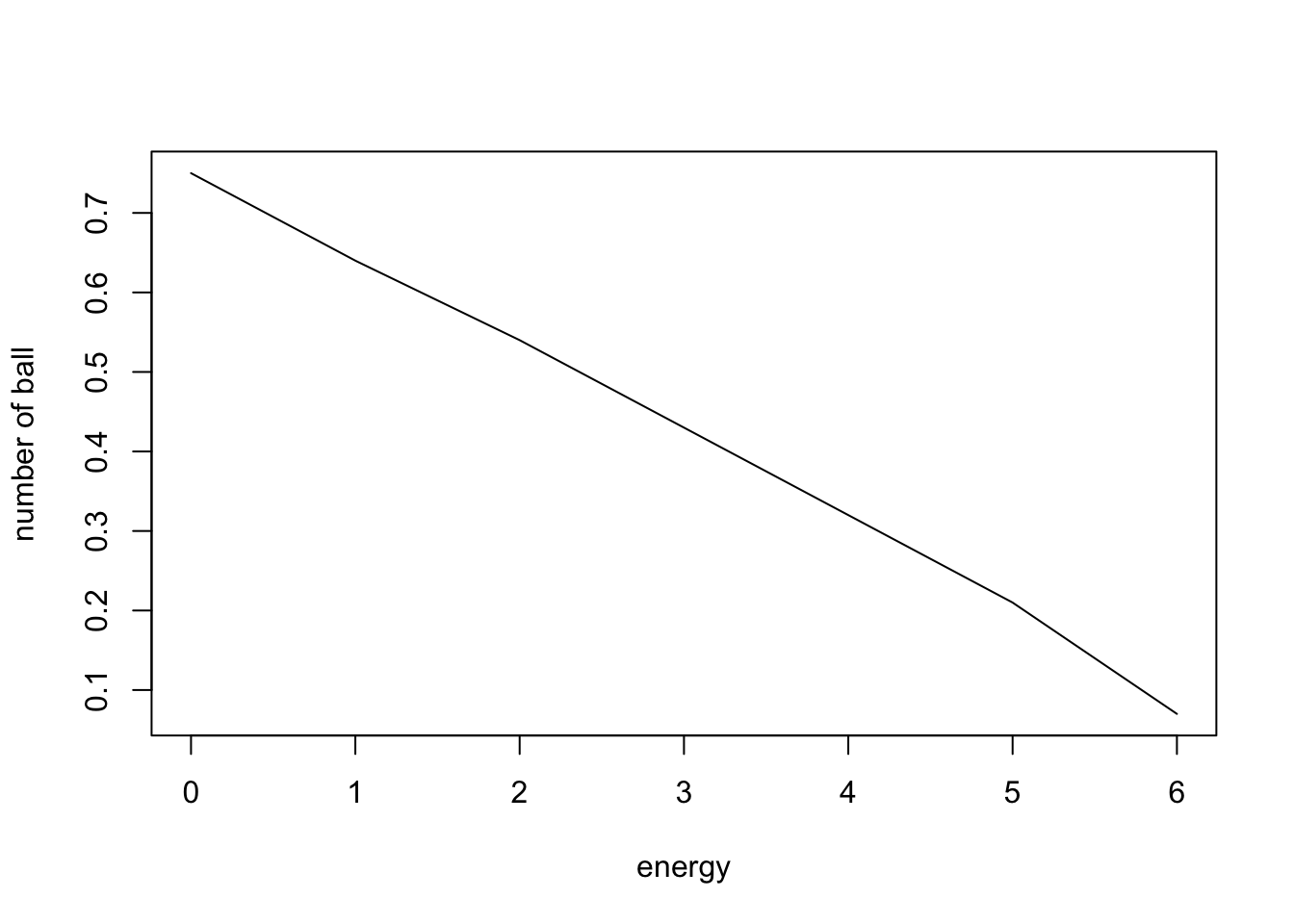
在这个演示里,能量分布似乎跟数目是线性的,但是如果我们把系统放宽,加入更多的球跟能量,这条曲线应该是指数分布的且指数为负。当然我知道你们不信,这里我们用 Eisberg & Resnick 在量子物理教材中描述来进行一个理论推导。
能量分布的数学形式
如果我们看到两个小球,这两个小球来自同一个能量分布,那么一个小球其出现在\(E_1\)上的概率为\(f(E_1)\),出现在\(E_2\)能量区间上的概率为\(f(E_2)\)。我们考虑一个特殊情况,一个小球来自\(E_1\)而另一个来自\(E_2\),发生这种情况的概率应该是两个概率的乘积,也就是:
\[ f(E_1) \times f(E_2) \]
然后,我们考虑所有宏观态中能量为\(E_1 + E_2\)的情况,因为我们进行了区间划分,所以能量为\(E_1 + E_2\)的情况只出现在所有能量和为这个数的小球组合里。由于我们之前假设了所有微观态是等概率的,那么出现这个能量和的小球组合方式也是等概率的。那么在某种程度上,会有下面的公式成立:
\[ f(E_1)+f(E_2) = h(E_1+E_2) \]
我们可以认为上面那个特殊情况,也就是一个小球来自\(E_1\)而另一个来自\(E_2\)的概率是属于\(E_1 + E_2\)这个能量分布的,那么根据第一段的推理出现这个情况时的概率应该是乘积。也就是两个能量和的出现概率既是两个独立能量区间概率的和又是乘积,那么满足这个条件的数学形式只能是指数形式。那么我们可以得出,在某个能量区间上小球的概率密度函数应该是:
\[ f(E) = A e^{-E/E_c} \]
这里面的常数\(E_c\)是描述独立于小球的系统变量,玻尔兹曼经过推导得出这一部分是系统温度(总能量)的线性函数,所以我们就有了玻尔兹曼分布的数学形式:
\[ f_b(E) = A e^{-E/kT} \]
这个分布描述了在封闭系统内不同能量的小球概率分布形式,简单说就是能量高的概率很低,而能量低的概率比较高。这个现象是客观存在的,但同时由于存在量子效应限制,有些能量段上的小球是无法稳定存在的,所以能谱分布实际并不连续,不过这就是另一个故事了。那么这个符合粒子运动的物理模型跟社会行为有什么联系呢?
社会行为
在一个达到平衡的社会经济系统中,我们对小球的假设基本是符合现实的,能量代表财富,那么很直观的现象就是这个社会的财富分配天然就不是平均的,会基本符合指数分布。也就是说,总是少数人富有而多数人穷。那么有人会反对说发达国家都是纺锤形的,明显模型有问题。没错,发达国家可以是纺锤的,但如果把全球看成一个缓慢增长的经济体,一个区域特别稳定富有只可能是牺牲其他区域的财富增长才能实现。所谓共同富裕,在全球封闭尺度下是无法自发形成的。这里看起来跟自由市场理论有矛盾,在自由市场下,看不见的手可以调节保证一个健康的经济发展,但在小球模型里经济并不发展,只是自由分配与交易。不过换句话,在经济停滞后的交易行为应该会导致更极端的财富分配。至于说自由市场里的自发交易可以促进合理的财富分配,我觉得比较扯,更靠谱是富有者所承担的社会文化压力,要不然亚当·斯密也不至于再去写一本《道德情操论》。
此外,请注意关键词:自发。也就是说不进行法律政策干预,但是如果博弈规则发生改变,那么物理系统就不那么好使了。另一个关键词是稳态,也就是如果社会整体财富增加了,那么即使分布不变,所有人生活的幸福指数也会提高。而增加社会整体财富的方式在最近这一百年的主要表现方式是科技革新,有意思的是,目前可以让财富分配更不平等的最主要动因也是科技的不平等。
在接下来的文章中,我们先看看到底这个世界的财富在不同的小球模型中会有如何的分布特征,然后再看看社会财富实际是如何分配的而物理学规律能给我们什么样的启发。