最近看到一系列以棒球为主题的关于贝叶斯分析的文章,赶忙总结了一下,省的忘了。我非常喜欢这类通过实际案例来进行分析的讲解方法,很容易举一反三。
什么是贝塔分布?
贝塔分布的本质是概率分布的分布。我们来看一个棒球击球率的估计问题,一共打了300个球,81个击中,219个击空。你可以计算出一个击中的概率:
\[\frac{\alpha}{\alpha + \beta} = \frac{81}{81+219} = 0.27\]
这个概率应该来自于一个分布,而这个分布可能是参数为 \(\alpha\) 与 \(\beta\) 的贝塔分布。我们看下概率密度曲线:
library(ggplot2)
x <- seq(0,1,length=100)
db <- dbeta(x, 81, 219)
ggplot() + geom_line(aes(x,db)) + ylab("Density of beta")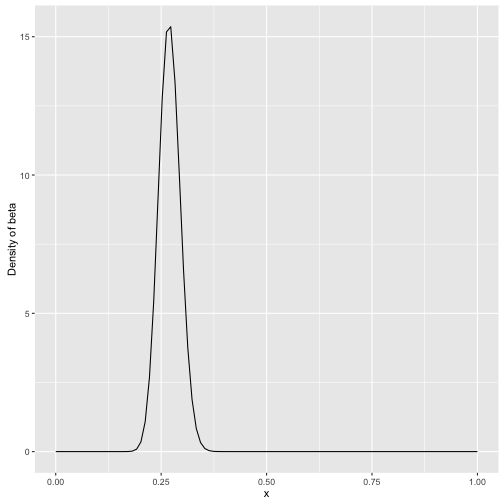
plot of chunk beta
观察这个概率密度分布图可以看出一个大约在0.2-0.35的概率区间,表示击球率可能的取值空间。
为什么击球的概率分布符合贝塔分布?
设想球员A打了一个球打中了,那么在没有先验知识的情况下我会认为他击中概率为1;这个球员又打中了一个球,那么还是1;但第三个没打中,我们会认为他击中概率是0吗?一般而言,这类连续击球问题可以用二项分布来描述,例如10个球打中8个的概率,我们假设这个击球概率为q,那么这个概率应该是个q的函数:
\[f(q) \propto q^a(1-q)^b\]
q对于一个实际问题(例如个人击球率)是常数,所以出现这个场景的概率实际上是a与b的函数。为了保障这个概率函数累积为1,需要除一个跟a与b有关的数。这个数可以用贝塔函数\(B(a,b)\)来表示,数学证明略。
那么我们继续关注这个球员,如果接着打了一个中了,那么如何更新这个概率?根据贝叶斯公式,最后推导出的结果如下:
\[Beta(\alpha+1,\beta+0)\]
根据公式可以看出我们对这个击球率的估计会高一点,这是贝塔分布的神奇之处,形式非常简单,理解也很直观。虽然贝塔分布不是为贝叶斯分析而设计的,但其数学性质非常便于进行贝叶斯分析。
先验与后验
如果我们后续观察的击球少,那么不太容易影响到对概率的先验估计:
x <- seq(0,1,length=100)
db <- dbeta(x, 81+1, 219)
ggplot() + geom_line(aes(x,db)) + ylab("Density of beta")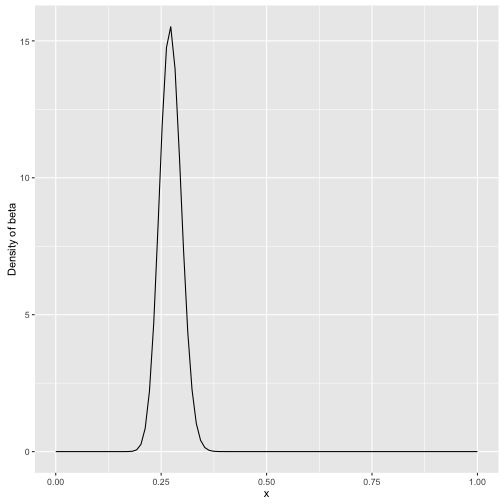
plot of chunk beta1
如果后续观察了大量的击球都中了,那么概率会偏向后面数据所提供的击球率:
x <- seq(0,1,length=100)
db <- dbeta(x, 81+1000, 219)
ggplot() + geom_line(aes(x,db)) + ylab("Density of beta")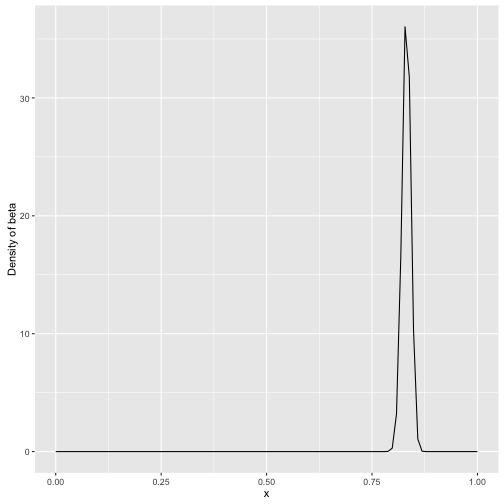
plot of chunk beta2
这是贝叶斯分析的核心思想,通过证据更新经验。经验是主观的或先验的,当证据足够多,结果就偏向事实。因此,最后得到的均值(后验0.83)一定是介于经验值(先验0.27)与证据值(全击中就是1)之间。
另一种不那么严谨的理解方法是如果一个概率是稳定的,那么多次实验的结果差别不会太大,则有:
\[\frac{a}{b} = \frac{c}{d} = \frac{a+b}{c+d}\]
如果每次实验的概率持平,那么不存在不确定度;但如果前面实验的次数少而后面实验的次数多,那么概率会偏重于后面,这就是贝塔分布想说明的事。
经验贝叶斯
对于两个球员,一个打了10个球中了4个,另一个打了1000个球中了300个,一般击中概率0.2,你会选哪一个去培养?我们对于小样本量的统计推断会有天然的不信任,如何通过统计量来描述?下面用MLB的数据说明,首先提取出球员的击球数据:
library(dplyr)
library(tidyr)
library(Lahman)
# 拿到击球数据
career <- Batting %>%
filter(AB > 0) %>%
anti_join(Pitching, by = "playerID") %>%
group_by(playerID) %>%
summarize(H = sum(H), AB = sum(AB)) %>%
mutate(average = H / AB)
# 把ID换成球员名字
career <- Master %>%
tbl_df() %>%
select(playerID, nameFirst, nameLast) %>%
unite(name, nameFirst, nameLast, sep = " ") %>%
inner_join(career, by = "playerID")
# 展示数据
career## Source: local data frame [9,342 x 5]
##
## playerID name H AB average
## (chr) (chr) (int) (int) (dbl)
## 1 aaronha01 Hank Aaron 3771 12364 0.3050
## 2 aaronto01 Tommie Aaron 216 944 0.2288
## 3 abadan01 Andy Abad 2 21 0.0952
## 4 abadijo01 John Abadie 11 49 0.2245
## 5 abbated01 Ed Abbaticchio 772 3044 0.2536
## 6 abbotfr01 Fred Abbott 107 513 0.2086
## 7 abbotje01 Jeff Abbott 157 596 0.2634
## 8 abbotku01 Kurt Abbott 523 2044 0.2559
## 9 abbotod01 Ody Abbott 13 70 0.1857
## 10 abercda01 Frank Abercrombie 0 4 0.0000
## .. ... ... ... ... ...# 击球前5
career %>%
arrange(desc(average)) %>%
head(5) %>%
kable()| playerID | name | H | AB | average |
|---|---|---|---|---|
| banisje01 | Jeff Banister | 1 | 1 | 1 |
| bassdo01 | Doc Bass | 1 | 1 | 1 |
| birasst01 | Steve Biras | 2 | 2 | 1 |
| burnscb01 | C. B. Burns | 1 | 1 | 1 |
| gallaja01 | Jackie Gallagher | 1 | 1 | 1 |
# 击球后5
career %>%
arrange(average) %>%
head(5) %>%
kable()| playerID | name | H | AB | average |
|---|---|---|---|---|
| abercda01 | Frank Abercrombie | 0 | 4 | 0 |
| adamsla01 | Lane Adams | 0 | 3 | 0 |
| allenho01 | Horace Allen | 0 | 7 | 0 |
| allenpe01 | Pete Allen | 0 | 4 | 0 |
| alstowa01 | Walter Alston | 0 | 1 | 0 |
如果仅考虑击球率会把很多板凳球员与运气球员包括进来,一个先验概率分布很有必要。那么考虑下如何得到,经验贝叶斯方法认为如果估计一个个体的参数,那么这个个体所在的整体的概率分布可作为先验概率分布。这个先验概率分布可以直接从数据的整体中得到,然后我们要用极大似然或矩估计的方法拿到贝塔分布的两个参数:
career_filtered <- career %>%
filter(AB >= 500)
m <- MASS::fitdistr(career_filtered$average, dbeta,
start = list(shape1 = 1, shape2 = 10))
alpha0 <- m$estimate[1]
beta0 <- m$estimate[2]
# 看下拟合效果
ggplot(career_filtered) +
geom_histogram(aes(average, y = ..density..), binwidth = .005) +
stat_function(fun = function(x) dbeta(x, alpha0, beta0), color = "red",
size = 1) +
xlab("Batting average")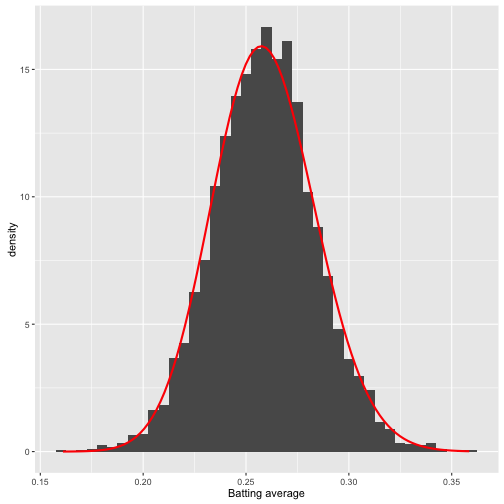
plot of chunk ebayes
当我们估计个人的击球率时,整体可以作为先验函数,个人的数据可以通过贝塔分布更新到个体。那么如果一个人数据少,我们倾向于认为他是平均水平;数据多则认为符合个人表现。这事实上是一个分层结构,贝叶斯推断里隐含了这么一个从整体到个人的过程
career_eb <- career %>%
mutate(eb_estimate = (H + alpha0) / (AB + alpha0 + beta0))
# 击球率高
career_eb %>%
arrange(desc(eb_estimate)) %>%
head(5) %>%
kable()| playerID | name | H | AB | average | eb_estimate |
|---|---|---|---|---|---|
| hornsro01 | Rogers Hornsby | 2930 | 8173 | 0.358 | 0.355 |
| jacksjo01 | Shoeless Joe Jackson | 1772 | 4981 | 0.356 | 0.350 |
| delahed01 | Ed Delahanty | 2596 | 7505 | 0.346 | 0.343 |
| hamilbi01 | Billy Hamilton | 2158 | 6268 | 0.344 | 0.340 |
| heilmha01 | Harry Heilmann | 2660 | 7787 | 0.342 | 0.338 |
# 击球率低
career_eb %>%
arrange(eb_estimate) %>%
head(5) %>%
kable()| playerID | name | H | AB | average | eb_estimate |
|---|---|---|---|---|---|
| bergebi01 | Bill Bergen | 516 | 3028 | 0.170 | 0.179 |
| oylerra01 | Ray Oyler | 221 | 1265 | 0.175 | 0.191 |
| vukovjo01 | John Vukovich | 90 | 559 | 0.161 | 0.196 |
| humphjo01 | John Humphries | 52 | 364 | 0.143 | 0.196 |
| bakerge01 | George Baker | 74 | 474 | 0.156 | 0.196 |
# 整体估计
ggplot(career_eb, aes(average, eb_estimate, color = AB)) +
geom_hline(yintercept = alpha0 / (alpha0 + beta0), color = "red", lty = 2) +
geom_point() +
geom_abline(color = "red") +
scale_colour_gradient(trans = "log", breaks = 10 ^ (1:5)) +
xlab("Batting average") +
ylab("Empirical Bayes batting average")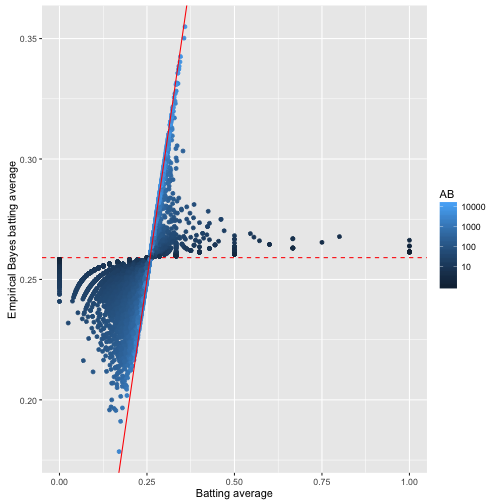
plot of chunk ebayes2
数据点多会收缩到\(x=y\),也就是个人的击球率;数据点少则回归到整体击球率。这就是经验贝叶斯方法的全貌:先估计整体的参数,然后把整体参数作为先验概率估计个人参数。
可信区间与置信区间
经验贝叶斯可以给出点估计,但现实中我们可能更关心区间估计,也就是击球率的范围。一般这类区间估计可以用二项式比例估计来进行,不过没有先验经验的限制置信区间会大到没意义。经验贝叶斯会给出一个后验分布,这个分布可以用来求可信区间。
# 给出后验分布
career_eb <- career %>%
mutate(eb_estimate = (H + alpha0) / (AB + alpha0 + beta0))
career_eb <- career_eb %>%
mutate(alpha1 = H + alpha0,
beta1 = AB - H + beta0)
# 提取洋基队的数据
yankee_1998 <- c("brosisc01", "jeterde01", "knoblch01", "martiti02", "posadjo01", "strawda01", "willibe02")
yankee_1998_career <- career_eb %>%
filter(playerID %in% yankee_1998)
# 展示球员的后验分布
library(broom)
yankee_beta <- yankee_1998_career %>%
inflate(x = seq(.18, .33, .0002)) %>%
ungroup() %>%
mutate(density = dbeta(x, alpha1, beta1))
ggplot(yankee_beta, aes(x, density, color = name)) +
geom_line() +
stat_function(fun = function(x) dbeta(x, alpha0, beta0),
lty = 2, color = "black")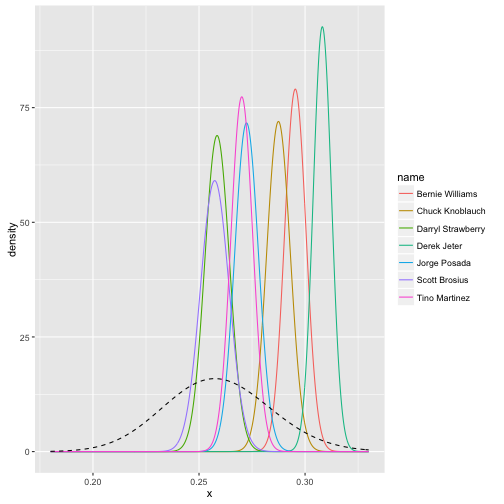
plot of chunk ci
# 提取可信区间
yankee_1998_career <- yankee_1998_career %>%
mutate(low = qbeta(.025, alpha1, beta1),
high = qbeta(.975, alpha1, beta1))
yankee_1998_career %>%
select(-alpha1, -beta1, -eb_estimate) %>%
knitr::kable()| playerID | name | H | AB | average | low | high |
|---|---|---|---|---|---|---|
| brosisc01 | Scott Brosius | 1001 | 3889 | 0.257 | 0.244 | 0.271 |
| jeterde01 | Derek Jeter | 3465 | 11195 | 0.310 | 0.300 | 0.317 |
| knoblch01 | Chuck Knoblauch | 1839 | 6366 | 0.289 | 0.277 | 0.298 |
| martiti02 | Tino Martinez | 1925 | 7111 | 0.271 | 0.260 | 0.280 |
| posadjo01 | Jorge Posada | 1664 | 6092 | 0.273 | 0.262 | 0.283 |
| strawda01 | Darryl Strawberry | 1401 | 5418 | 0.259 | 0.247 | 0.270 |
| willibe02 | Bernie Williams | 2336 | 7869 | 0.297 | 0.286 | 0.305 |
# 绘制可信区间
yankee_1998_career %>%
mutate(name = reorder(name, average)) %>%
ggplot(aes(average, name)) +
geom_point() +
geom_errorbarh(aes(xmin = low, xmax = high)) +
geom_vline(xintercept = alpha0 / (alpha0 + beta0), color = "red", lty = 2) +
xlab("Estimated batting average (w/ 95% interval)") +
ylab("Player")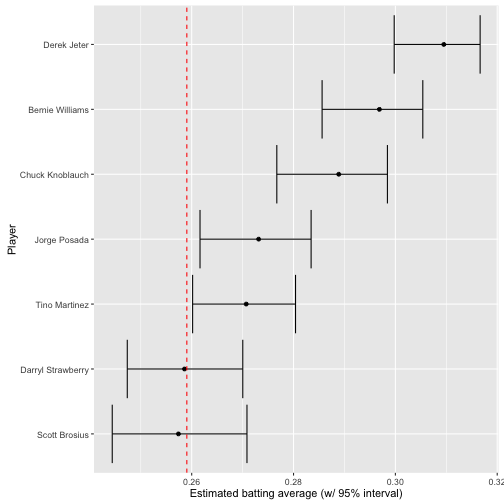
plot of chunk ci
# 对比置信区间与可信区间
career_eb <- career_eb %>%
mutate(low = qbeta(.025, alpha1, beta1),
high = qbeta(.975, alpha1, beta1))
set.seed(2016)
some <- career_eb %>%
sample_n(20) %>%
mutate(name = paste0(name, " (", H, "/", AB, ")"))
frequentist <- some %>%
group_by(playerID, name, AB) %>%
do(tidy(binom.test(.$H, .$AB))) %>%
select(playerID, name, estimate, low = conf.low, high = conf.high) %>%
mutate(method = "Confidence")
bayesian <- some %>%
select(playerID, name, AB, estimate = eb_estimate,
low = low, high = high) %>%
mutate(method = "Credible")
combined <- bind_rows(frequentist, bayesian)
combined %>%
mutate(name = reorder(name, -AB)) %>%
ggplot(aes(estimate, name, color = method, group = method)) +
geom_point() +
geom_errorbarh(aes(xmin = low, xmax = high)) +
geom_vline(xintercept = alpha0 / (alpha0 + beta0), color = "red", lty = 2) +
xlab("Estimated batting average") +
ylab("Player") +
labs(color = "")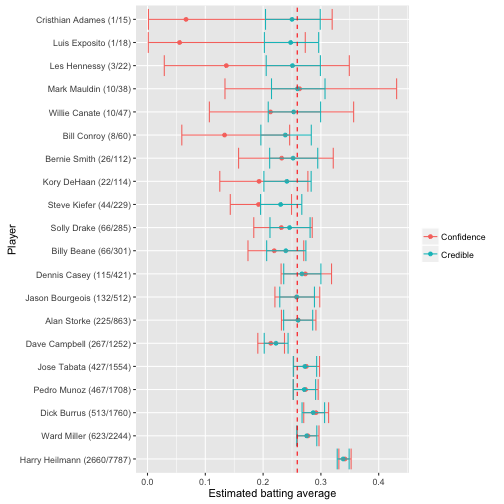
plot of chunk ci
可信区间与置信区间(二项式比例估计)很大的区别在于前者考虑了先验概率进而实现了区间的收缩,后者则可看作无先验贝塔分布给出的区间估计,频率学派目前没有很好的收缩区间估计的方法。
后验错误率
现实问题经常不局限于估计,而是侧重决策,例如如果一个球员的击球率高于某个值,他就可以进入名人堂(击球率大于0.3),这个决策常常伴随区间估计而不是简单的点估计:
# 以 Hank Aaron 为例
career_eb %>%
filter(name == "Hank Aaron") %>%
do(data_frame(x = seq(.27, .33, .0002),
density = dbeta(x, .$alpha1, .$beta1))) %>%
ggplot(aes(x, density)) +
geom_line() +
geom_ribbon(aes(ymin = 0, ymax = density * (x < .3)),
alpha = .1, fill = "red") +
geom_vline(color = "red", lty = 2, xintercept = .3)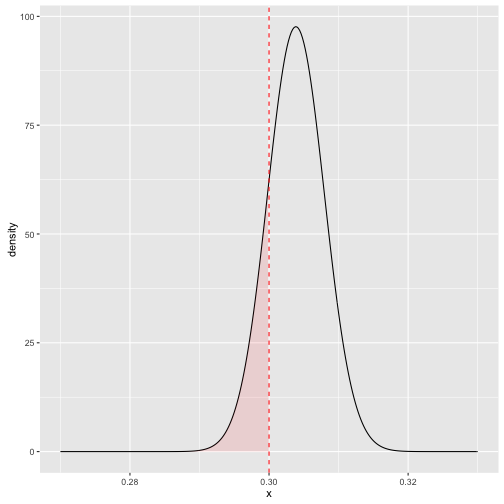
plot of chunk lp
# 提取该球员数据
career_eb %>% filter(name == "Hank Aaron")## Source: local data frame [1 x 10]
##
## playerID name H AB average eb_estimate alpha1 beta1 low
## (chr) (chr) (int) (int) (dbl) (dbl) (dbl) (dbl) (dbl)
## 1 aaronha01 Hank Aaron 3771 12364 0.305 0.304 3850 8819 0.296
## Variables not shown: high (dbl)# 计算其不进入名人堂的概率
pbeta(.3, 3850, 8818)## [1] 0.169这里我们引入后验错误率与后验包括率两个概念。后验错误率(Posterior Error Probability)可类比经典假设检验中的显著性水平\(\alpha\);后验包括率(Posterior Inclusion Probability)可类比经典假设检验中的置信水平\(1-\alpha\)
# 所有球员的后验错误率分布,大部分不超过0.3
career_eb <- career_eb %>%
mutate(PEP = pbeta(.3, alpha1, beta1))
ggplot(career_eb, aes(PEP)) +
geom_histogram(binwidth = .02) +
xlab("Posterior Error Probability (PEP)") +
xlim(0, 1)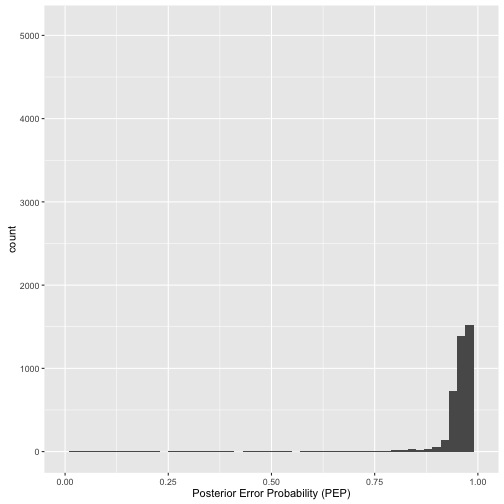
plot of chunk ap
# 后验错误率与击球率的关系
career_eb %>%
ggplot(aes(eb_estimate, PEP, color = AB)) +
geom_point(size = 1) +
xlab("(Shrunken) batting average estimate") +
ylab("Posterior Error Probability (PEP)") +
geom_vline(color = "red", lty = 2, xintercept = .3) +
scale_colour_gradient(trans = "log", breaks = 10 ^ (1:5))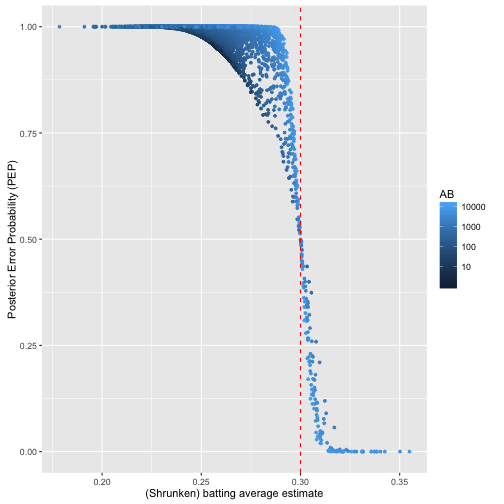
plot of chunk ap
后验错误率高于0.3的多数是击球率与击球数都高的人,因为经验贝叶斯方法惩罚了击球数低的人。
错误发现率(FDR)
错误发现率可用来控制一个整体决策,保证整体犯错的概率低于某个数值,错误发现率越高,越可能把假阳性包括进来。假如我们把进入名人堂的决策作为一个整体,则可允许一定的整体错误率,因为每个人的后验错误率可以计算且期望值线性可加和,我们可以得到一个整体的错误率:
# 取前100个球员
top_players <- career_eb %>%
arrange(PEP) %>%
head(100)
# 总错率率
sum(top_players$PEP)## [1] 4.69# 平均错误率
mean(top_players$PEP)## [1] 0.0469# 错误率随所取球员的变化
sorted_PEP <- career_eb %>%
arrange(PEP)
mean(head(sorted_PEP$PEP, 50))## [1] 0.00113mean(head(sorted_PEP$PEP, 200))## [1] 0.241错误率在排序后前面低后面高,但这个错误率不特指某个球员,而是包含到某个球员的整体犯错的概率。
q值
q值定义为排序后累积到某个样本的整体平均错误率,类似多重比较中对整体错误率控制的p值。
# 生成每个球员的q值
career_eb <- career_eb %>%
arrange(PEP) %>%
mutate(qvalue = cummean(PEP))
# 观察不同q值对名人堂球员数的影响
career_eb %>%
ggplot(aes(qvalue, rank(PEP))) +
geom_line() +
xlab("q-value cutoff") +
ylab("Number of players included")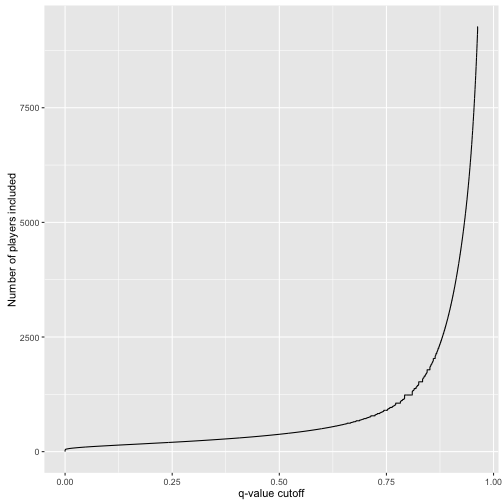
plot of chunk qvalue
# 观察小q值部分
career_eb %>%
filter(qvalue < .25) %>%
ggplot(aes(qvalue, rank(PEP))) +
geom_line() +
xlab("q-value cutoff") +
ylab("Number of players included")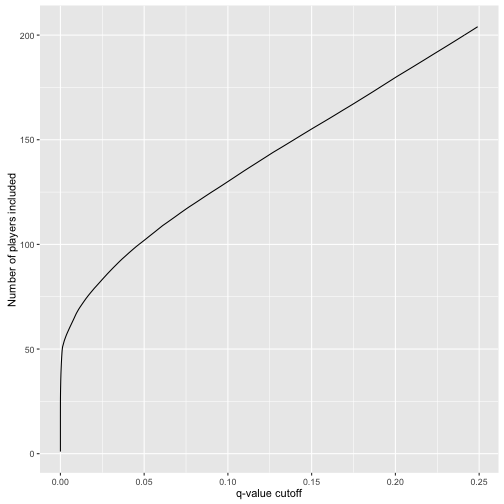
plot of chunk qvalue
200个人进入名人堂可能有1/4的球员不合适,如果是50个人进入名人堂那么基本不会犯错。
q值是一个整体而非个体的平均错误率,具有累积性,不代表q值大的那一个就是错的。q值在频率学派的多重比较里也有定义,虽然没有空假设(有先验概率),但实质等同。
贝叶斯视角下的假设检验
前面描述的是击球率如何求,如何进行区间估计与多个体的错误率控制,面向的个体或整体,那么如何解决比较问题。设想多个球员,我们考虑如何去比较他们击球率:
# 选三个球员
career_eb %>%
filter(name %in% c("Hank Aaron", "Mike Piazza", "Hideki Matsui")) %>%
inflate(x = seq(.26, .33, .00025)) %>%
mutate(density = dbeta(x, alpha1, beta1)) %>%
ggplot(aes(x, density, color = name)) +
geom_line() +
labs(x = "Batting average", color = "")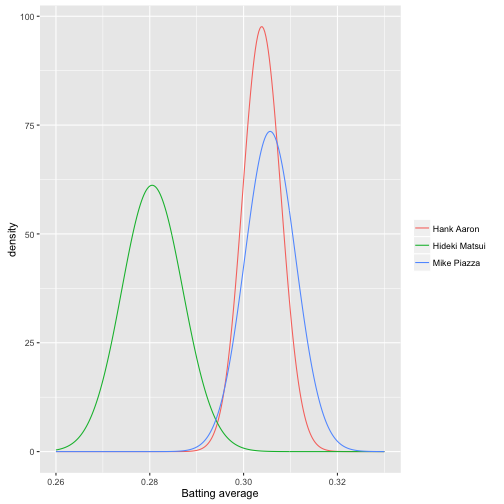
plot of chunk ht
如果两个球员击球率的概率密度曲线比较接近,那么即便均值有不同我们也无法进行区分;如果重叠比较少,那么我们有理由认为他们之间的差异显著。那么贝叶斯视角下如何定量描述这个差异是否显著?
模拟
单纯取样比大小然后计算比例:
# 提取两人数据
aaron <- career_eb %>% filter(name == "Hank Aaron")
piazza <- career_eb %>% filter(name == "Mike Piazza")
# 模拟取样10万次
piazza_simulation <- rbeta(1e6, piazza$alpha1, piazza$beta1)
aaron_simulation <- rbeta(1e6, aaron$alpha1, aaron$beta1)
# 计算一个人超过另一个人的概率
sim <- mean(piazza_simulation > aaron_simulation)
sim## [1] 0.606数值积分
两个概率的联合概率分布,然后积分一个球员大于另一个的概率:
d <- .00002
limits <- seq(.29, .33, d)
sum(outer(limits, limits, function(x, y) {
(x > y) *
dbeta(x, piazza$alpha1, piazza$beta1) *
dbeta(y, aaron$alpha1, aaron$beta1) *
d ^ 2
}))## [1] 0.604解析解
两个贝塔分布一个比另一个高是有含有贝塔函数的解析解的:
\[p_A \sim \mbox{Beta}(\alpha_A, \beta_A)\]
\[p_B \sim \mbox{Beta}(\alpha_B, \beta_B)\]
\[{\rm Pr}(p_B > p_A) = \sum_{i=0}^{\alpha_B-1}\frac{B(\alpha_A+i,\beta_A+\beta_B)}{(\beta_B+i) B(1+i, \beta_B) B(\alpha_A, \beta_A) }\]
h <- function(alpha_a, beta_a,
alpha_b, beta_b) {
j <- seq.int(0, round(alpha_b) - 1)
log_vals <- (lbeta(alpha_a + j, beta_a + beta_b) - log(beta_b + j) -
lbeta(1 + j, beta_b) - lbeta(alpha_a, beta_a))
1 - sum(exp(log_vals))
}
h(piazza$alpha1, piazza$beta1,
aaron$alpha1, aaron$beta1)## [1] 0.605正态近似求解
贝塔分布在\(\alpha\)与\(\beta\)比较大时接近正态分布,可以直接用正态分布的解析解求,速度快很多:
h_approx <- function(alpha_a, beta_a,
alpha_b, beta_b) {
u1 <- alpha_a / (alpha_a + beta_a)
u2 <- alpha_b / (alpha_b + beta_b)
var1 <- alpha_a * beta_a / ((alpha_a + beta_a) ^ 2 * (alpha_a + beta_a + 1))
var2 <- alpha_b * beta_b / ((alpha_b + beta_b) ^ 2 * (alpha_b + beta_b + 1))
pnorm(0, u2 - u1, sqrt(var1 + var2))
}
h_approx(piazza$alpha1, piazza$beta1, aaron$alpha1, aaron$beta1)## [1] 0.606比例检验
这是个列联表问题,频率学派对比两个比例:
two_players <- bind_rows(aaron, piazza)
two_players %>%
transmute(Player = name, Hits = H, Misses = AB - H) %>%
knitr::kable()| Player | Hits | Misses |
|---|---|---|
| Hank Aaron | 3771 | 8593 |
| Mike Piazza | 2127 | 4784 |
prop.test(two_players$H, two_players$AB)##
## 2-sample test for equality of proportions with continuity
## correction
##
## data: two_players$H out of two_players$AB
## X-squared = 0.1, df = 1, p-value = 0.7
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## -0.0165 0.0109
## sample estimates:
## prop 1 prop 2
## 0.305 0.308贝叶斯学派对比两个比例:
credible_interval_approx <- function(a, b, c, d) {
u1 <- a / (a + b)
u2 <- c / (c + d)
var1 <- a * b / ((a + b) ^ 2 * (a + b + 1))
var2 <- c * d / ((c + d) ^ 2 * (c + d + 1))
mu_diff <- u2 - u1
sd_diff <- sqrt(var1 + var2)
data_frame(posterior = pnorm(0, mu_diff, sd_diff),
estimate = mu_diff,
conf.low = qnorm(.025, mu_diff, sd_diff),
conf.high = qnorm(.975, mu_diff, sd_diff))
}
credible_interval_approx(piazza$alpha1, piazza$beta1, aaron$alpha1, aaron$beta1)## Source: local data frame [1 x 4]
##
## posterior estimate conf.low conf.high
## (dbl) (dbl) (dbl) (dbl)
## 1 0.606 -0.00182 -0.0151 0.0115多个球员对比一个:
set.seed(2016)
intervals <- career_eb %>%
filter(AB > 10) %>%
sample_n(20) %>%
group_by(name, H, AB) %>%
do(credible_interval_approx(piazza$alpha1, piazza$beta1, .$alpha1, .$beta1)) %>%
ungroup() %>%
mutate(name = reorder(paste0(name, " (", H, " / ", AB, ")"), -estimate))
f <- function(H, AB) broom::tidy(prop.test(c(H, piazza$H), c(AB, piazza$AB)))
prop_tests <- purrr::map2_df(intervals$H, intervals$AB, f) %>%
mutate(estimate = estimate1 - estimate2,
name = intervals$name)
all_intervals <- bind_rows(
mutate(intervals, type = "Credible"),
mutate(prop_tests, type = "Confidence")
)
ggplot(all_intervals, aes(x = estimate, y = name, color = type)) +
geom_point() +
geom_errorbarh(aes(xmin = conf.low, xmax = conf.high)) +
xlab("Piazza average - player average") +
ylab("Player")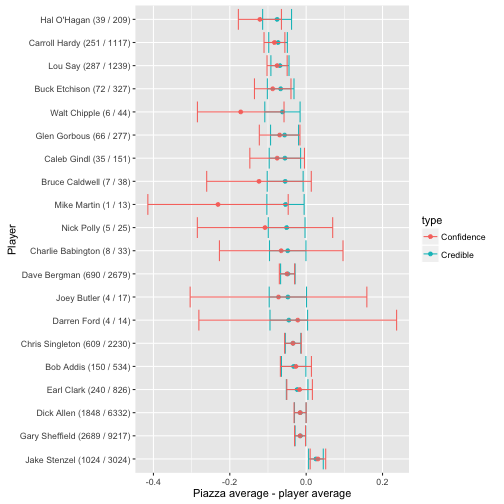
plot of chunk mp
由此,置信区间与可信区间的主要差异来自于经验贝叶斯的区间收敛,也就是对整体先验概率的考虑。
错误率控制
如果我打算交易一个球员,那么如何筛选候选人?肯定是先选那些击球率更好的球员:
# 对比打算交易的球员与其他球员
career_eb_vs_piazza <- bind_cols(
career_eb,
credible_interval_approx(piazza$alpha1, piazza$beta1,
career_eb$alpha1, career_eb$beta1)) %>%
select(name, posterior, conf.low, conf.high)
career_eb_vs_piazza## Source: local data frame [9,342 x 4]
##
## name posterior conf.low conf.high
## (chr) (dbl) (dbl) (dbl)
## 1 Rogers Hornsby 2.84e-11 0.0345 0.0639
## 2 Ed Delahanty 7.10e-07 0.0218 0.0518
## 3 Shoeless Joe Jackson 8.77e-08 0.0278 0.0611
## 4 Willie Keeler 4.62e-06 0.0183 0.0472
## 5 Nap Lajoie 1.62e-05 0.0158 0.0441
## 6 Tony Gwynn 1.83e-05 0.0157 0.0442
## 7 Harry Heilmann 7.19e-06 0.0180 0.0476
## 8 Lou Gehrig 1.43e-05 0.0167 0.0461
## 9 Billy Hamilton 7.03e-06 0.0190 0.0502
## 10 Eddie Collins 2.00e-04 0.0113 0.0393
## .. ... ... ... ...# 计算q值
career_eb_vs_piazza <- career_eb_vs_piazza %>%
arrange(posterior) %>%
mutate(qvalue = cummean(posterior))
# 筛选那些q值小于0.05的
better <- career_eb_vs_piazza %>%
filter(qvalue < .05)
better## Source: local data frame [50 x 5]
##
## name posterior conf.low conf.high qvalue
## (chr) (dbl) (dbl) (dbl) (dbl)
## 1 Rogers Hornsby 2.84e-11 0.0345 0.0639 2.84e-11
## 2 Shoeless Joe Jackson 8.77e-08 0.0278 0.0611 4.39e-08
## 3 Ed Delahanty 7.10e-07 0.0218 0.0518 2.66e-07
## 4 Willie Keeler 4.62e-06 0.0183 0.0472 1.36e-06
## 5 Billy Hamilton 7.03e-06 0.0190 0.0502 2.49e-06
## 6 Harry Heilmann 7.19e-06 0.0180 0.0476 3.27e-06
## 7 Lou Gehrig 1.43e-05 0.0167 0.0461 4.85e-06
## 8 Nap Lajoie 1.62e-05 0.0158 0.0441 6.28e-06
## 9 Tony Gwynn 1.83e-05 0.0157 0.0442 7.62e-06
## 10 Bill Terry 3.03e-05 0.0162 0.0472 9.89e-06
## .. ... ... ... ... ...这样我们筛到一个可交易的群体,总和错误率不超过5%。
影响因子
击球率高还有可能是因为得到的机会多或者光环效应,一开始凭运气打得好,后面给机会多,通过经验累积提高了击球率:
career %>%
filter(AB >= 20) %>%
ggplot(aes(AB, average)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
scale_x_log10()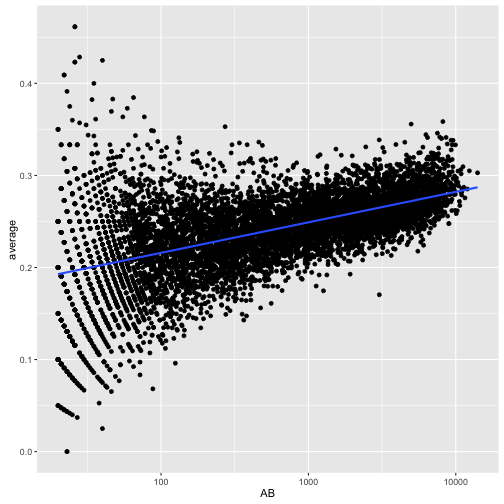
plot of chunk if
击球数低方差会大,这比较正常,很多人挂在起跑线上了。直接使用经验贝叶斯方法会导致整体向均值收敛,这高估了新手的数据:
prior_mu <- alpha0 / (alpha0 + beta0)
career_eb %>%
filter(AB >= 20) %>%
gather(type, value, average, eb_estimate) %>%
mutate(type = plyr::revalue(type, c(average = "Raw",
eb_estimate = "With EB Shrinkage"))) %>%
ggplot(aes(AB, value)) +
geom_point() +
scale_x_log10() +
geom_hline(color = "red", lty = 2, size = 1.5, yintercept = prior_mu) +
facet_wrap(~type) +
ylab("average") +
geom_smooth(method = "lm")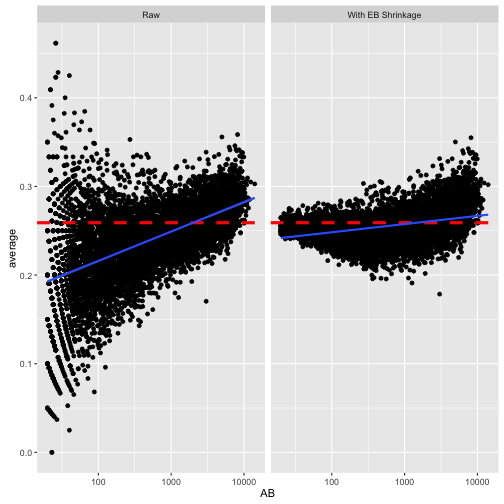
plot of chunk ife
为了如实反应这种情况,我们应该认为击球率符合贝塔分布,但同时贝塔分布的两个参数受击球数的影响,击球数越多,越可能击中。这个模型可以用贝塔-二项式回归来描述:
\[\mu_i = \mu_0 + \mu_{\mbox{AB}} \cdot \log(\mbox{AB})\]
\[\alpha_{0,i} = \mu_i / \sigma_0\]
\[\beta_{0,i} = (1 - \mu_i) / \sigma_0\]
\[p_i \sim \mbox{Beta}(\alpha_{0,i}, \beta_{0,i})\]
\[H_i \sim \mbox{Binom}(\mbox{AB}_i, p_i)\]
拟合模型
寻找拟合后的模型参数,构建新的先验概率:
library(gamlss)
# 拟合模型
fit <- gamlss(cbind(H, AB - H) ~ log(AB),
data = career_eb,
family = BB(mu.link = "identity"))## GAMLSS-RS iteration 1: Global Deviance = 91083
## GAMLSS-RS iteration 2: Global Deviance = 72051
## GAMLSS-RS iteration 3: Global Deviance = 67972
## GAMLSS-RS iteration 4: Global Deviance = 67966
## GAMLSS-RS iteration 5: Global Deviance = 67966library(broom)
# 展示拟合参数
td <- tidy(fit)
td## parameter term estimate std.error statistic p.value
## 1 mu (Intercept) 0.1441 0.001616 89.1 0
## 2 mu log(AB) 0.0151 0.000221 68.5 0
## 3 sigma (Intercept) -6.3372 0.024910 -254.4 0# 构建新的先验概率
mu_0 <- td$estimate[1]
mu_AB <- td$estimate[2]
sigma <- exp(td$estimate[3])
# 看看AB对先验概率的影响
crossing(x = seq(0.08, .35, .001), AB = c(1, 10, 100, 1000, 10000)) %>%
mutate(density = dbeta(x, (mu_0 + mu_AB * log(AB)) / sigma,
(1 - (mu_0 + mu_AB * log(AB))) / sigma)) %>%
mutate(AB = factor(AB)) %>%
ggplot(aes(x, density, color = AB, group = AB)) +
geom_line() +
xlab("Batting average") +
ylab("Prior density")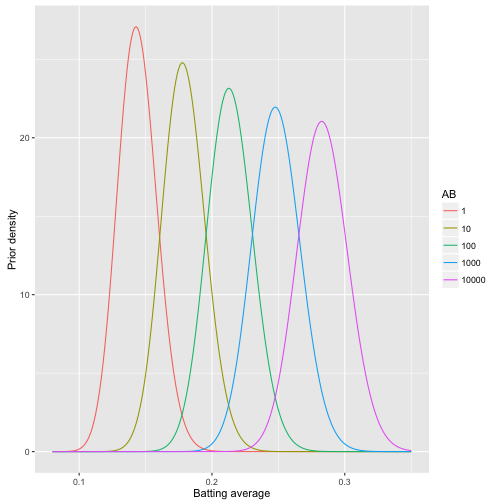
plot of chunk fitbb
求后验概率
# 计算所有拟合值
mu <- fitted(fit, parameter = "mu")
sigma <- fitted(fit, parameter = "sigma")
# 计算所有后验概率
career_eb_wAB <- career_eb %>%
dplyr::select(name, H, AB, original_eb = eb_estimate) %>%
mutate(mu = mu,
alpha0 = mu / sigma,
beta0 = (1 - mu) / sigma,
alpha1 = alpha0 + H,
beta1 = beta0 + AB - H,
new_eb = alpha1 / (alpha1 + beta1))
# 展示拟合后的击球率
ggplot(career_eb_wAB, aes(original_eb, new_eb, color = AB)) +
geom_point() +
geom_abline(color = "red") +
xlab("Original EB Estimate") +
ylab("EB Estimate w/ AB term") +
scale_color_continuous(trans = "log", breaks = 10 ^ (0:4))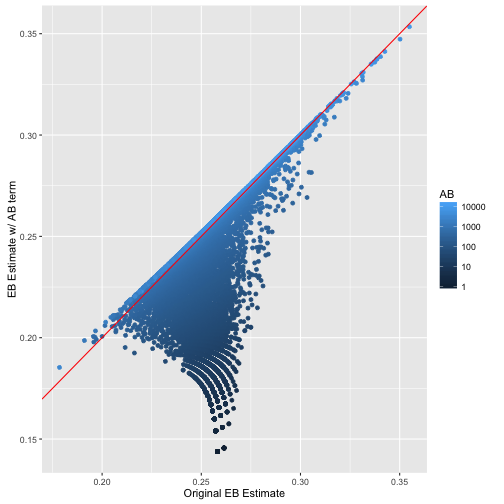
plot of chunk fitpo
# 对比
library(tidyr)
lev <- c(raw = "Raw H / AB", original_eb = "EB Estimate", new_eb = "EB w/ Regression")
career_eb_wAB %>%
filter(AB >= 10) %>%
mutate(raw = H / AB) %>%
gather(type, value, raw, original_eb, new_eb) %>%
mutate(mu = ifelse(type == "original_eb", prior_mu,
ifelse(type == "new_eb", mu, NA))) %>%
mutate(type = factor(plyr::revalue(type, lev), lev)) %>%
ggplot(aes(AB, value)) +
geom_point() +
geom_line(aes(y = mu), color = "red") +
scale_x_log10() +
facet_wrap(~type) +
xlab("At-Bats (AB)") +
ylab("Estimate")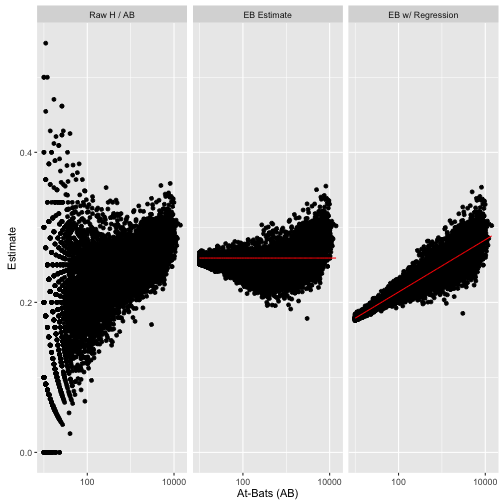
plot of chunk fitpo
矫正后我们的数据更复合现实了,其实这是贝叶斯分层模型的一个简单版本,通过考虑更多因素,我们可以构建更复杂的模型来挖掘出我们所需要的信息。