安斯库姆四重奏算得上数据可视化里最经典的案例了,四组不同的数据做线性相关,得到相关系数一样(0.816)但实际作图可以看出很大差异。
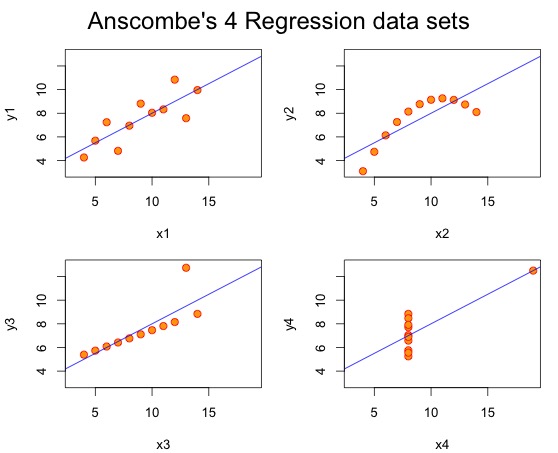
第一次看到这图的时候有人就说这辈子能搞出个类似的数据集就名留青史了,而我当时觉得作为一个外行这辈子能再看到个类似的可视化案例也算不虚此生了,前天还真看到了。
Plos Biology 上刚发表了一篇PERSPECTIVE来吐槽条形图,作者收集了2014年一季度前25%的生理学期刊中发表的703篇文章并对其中的图像进行了统计。结果如下:
- 条形图是这些文章作者最喜欢的图形展示方法,85.6%的文章包含至少一张条形图
- 77.6%的条形图使用的是均值配合标准误,15.3%使用均值配合标准差
- 61.3%的文章使用线图,散点图配合误差线,误差多数使用标准误
- 使用直方图,散点图与箱式图等展示数据分布的不到五分之一
然后作者开始吐槽了:
- 你们懂不懂啥时候用SD啥时候用SE啊
- 不懂没关系啊,反正都不该用啊
- 那些都是描述性统计啊,你样本那么少直接画出来多好,算什么均值啊
- 展示数据跟假设检验两个概念,别混了啊
- 做对比用t检验你查过数据分布了吗?有异常值检验啊
- 不会没关系啊,反正我建议用非参方法啊,当然我知道损失功效啊
- 用非参方法要展示中值啊,中值的差跟差的中值不是一回事啊
上面这些缺少直观理解,请看下图:
散点图完全不同的数据画成条形图是一样的,误差线一样长,看下面的检验结果,参数方法与非参方法完全不同。这副图与安斯库姆四重奏有异曲同工之处,本质上都是在表示没有图形展示的假设检验可能会遗漏重要信息。其实对于一个实验设计良好的工作是不该出现上面的问题的,但现在很多人在论文撰写或数据展示及检验时喜欢套用别人的展示方法,完全不明就里。更尴尬的是你就算告诉他们数据有问题,他们也不知道怎么改,非参方法要么没听说过,要么仅仅是听说过没用过。至于数据展示,这种所谓 Univariate scatterplots 的图根本不知道怎么画,不过作者算得上宅心仁厚,亲自做了一个excel模版供其他人使用。
其实类似的图形也有如下的展示分布的方法(附注R代码),但数据太少时就别考虑了,垃圾进,垃圾出。
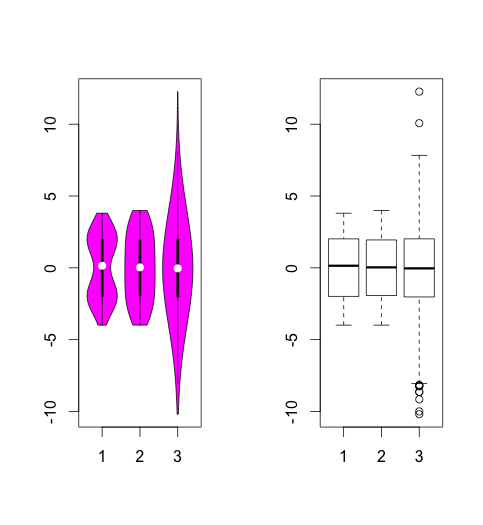
- 小提琴图
par(mfrow=c(1,2))
mu<-2
si<-0.6
bimodal<-c(rnorm(1000,-mu,si),rnorm(1000,mu,si))
uniform<-runif(2000,-4,4)
normal<-rnorm(2000,0,3)
vioplot(bimodal,uniform,normal)
boxplot(bimodal,uniform,normal)
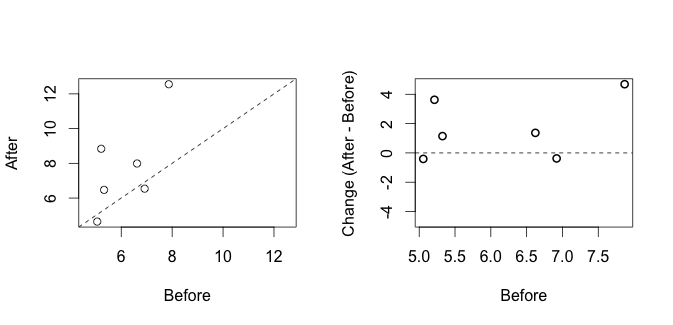
- 差异散点图
# 这个太简单了,就是当要展示的两组数据为配对数据时,直接对其差异作普通散点图并附上参考线
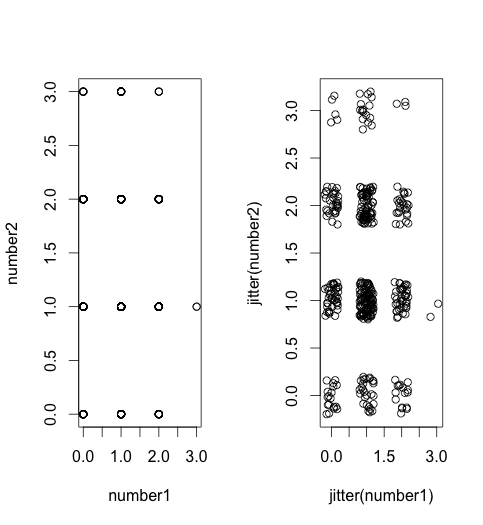
- 抖动散点图
number1 <- rhyper(400,3,6,3)
number2 <- rhyper(400,4,5,3)
par(mfrow=c(1,2))
plot(number1,number2)
plot(jitter(number1),jitter(number2))
- 平滑散点图
par(mfrow=c(1,1))
number1 <- rhyper(30,4,5,4)
number2 <- rhyper(30,4,5,4)
smoothScatter(number1,number2)
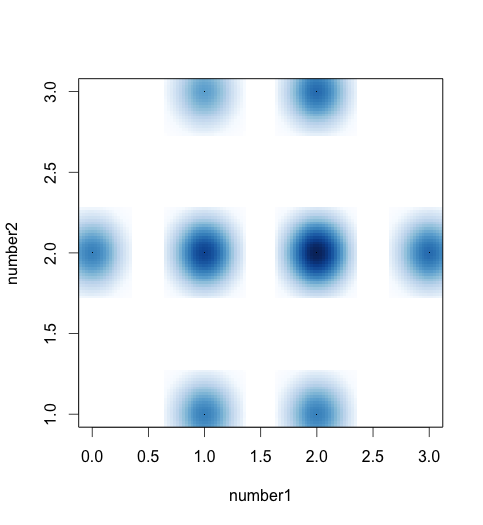
其实数据展示在能表意清晰的条件下越原始越好,这样能更好的展示原始数据的意义,如果加入过多的总结性描述,总有种隐藏信息的感觉。
参考文献
Beyond Bar and Line Graphs: Time for a New Data Presentation Paradigm(开放获取)