最近看到一篇论文,作者利用微博关键词出现的频率来预测空气污染的状况并认为来自社交媒体的数据能为环境监测提供更多的细节。这个想法很不错,但其实抛开文章的视角,微博的文本分析技术上实现并不困难,下面以齐普夫定律的验证做一个展示。
首先找一个开源的微博语料库,我找到的是NLPIR微博内容语料库,里面有23万条微博内容。然后从里面提取词汇与词频,目的是用来验证下文献计量学中的齐普夫定律,也就是发现字词的使用次数(f)与字词的使次数排名(r)之乘积,会等于常数C。
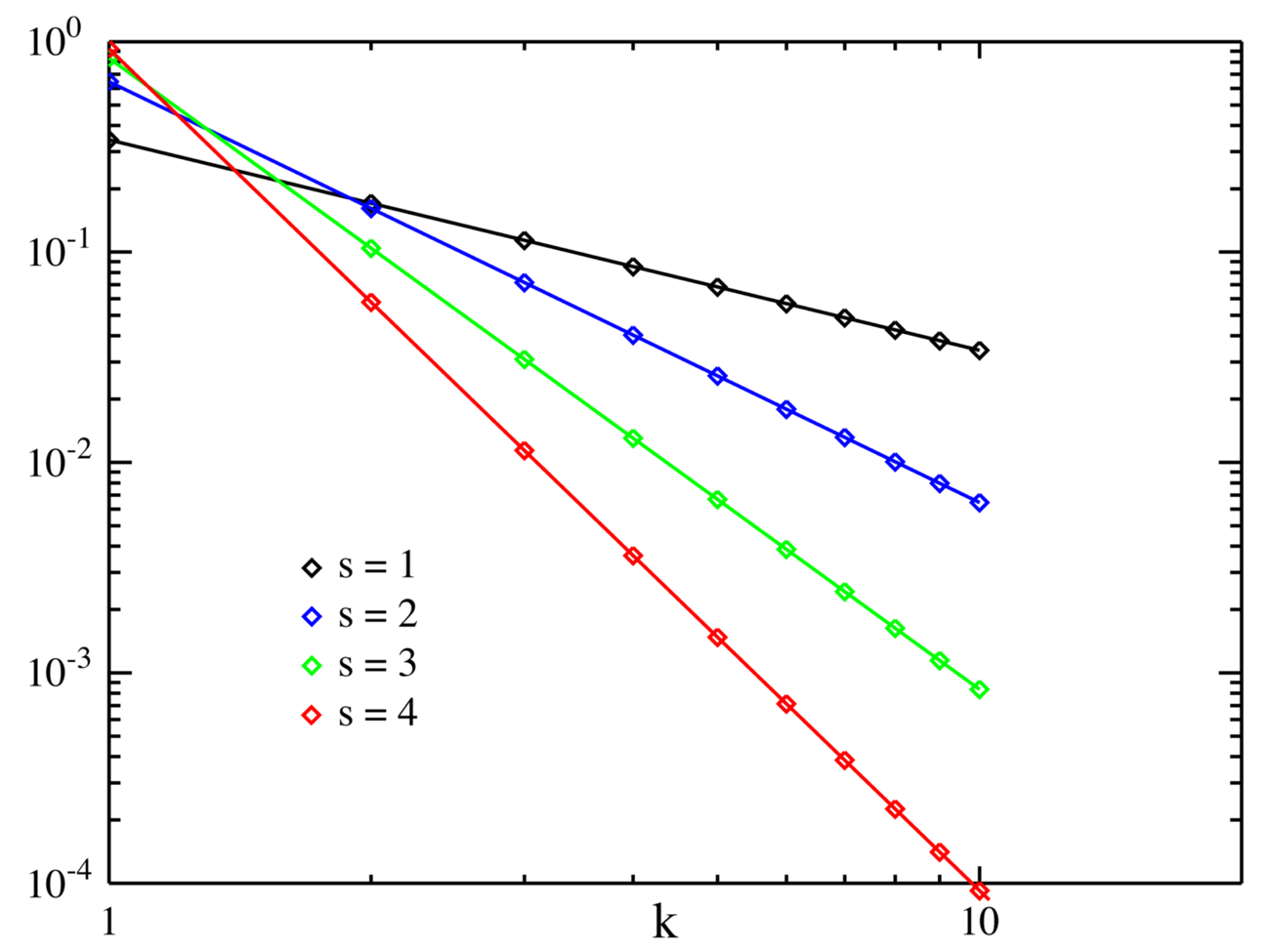
上图来自维基百科
分析代码
以下代码可在下载数据并设定数据路径后重复。
# 读入xml包
library(XML)
# 读取数据并提取文本信息
doc <- xmlTreeParse('NLPIR微博内容语料库.xml',useInternal=TRUE)
rootNode <- xmlRoot(doc)
doc1 <- xpathSApply(rootNode,"//article",xmlValue)
# 去除无关标点与数字
doc2 <- gsub(pattern="http:[a-zA-Z\\/\\.0-9]+","",doc1)
# 中文分词
library(Rwordseg)
doc3 <- segmentCN(doc2)
# 构建语料库 去掉标点与数字与高频词
library(tm)
doc4 <- Corpus(VectorSource(doc3))
doc5 <- tm_map(doc4, removePunctuation)
doc6 <- tm_map(doc5, removeNumbers)
# 高频无意义词在这里可以搞到 https://github.com/yufree/democode/tree/master/data
x <- scan("stopwords.txt", what="")
doc7 <- tm_map(doc6, removeWords, x)
doc8 <- tm_map(doc7, stripWhitespace)
# 构建全范围的词频矩阵
control=list(minDocFreq=5,wordLengths = c(1, Inf),bounds = list(global = c(5,Inf)),weighting = weightTf,encoding = 'UTF-8')
doc.tdm=TermDocumentMatrix(doc8,control)
# 这里截取词频高于5长度为2的词
control2=list(minDocFreq=5,wordLengths = c(2, 2),bounds = list(global = c(5,Inf)),weighting = weightTf,encoding = 'UTF-8')
doc.tdm2=TermDocumentMatrix(doc8,control2)
# 这里截取词频高于5长度为3的词
control3=list(minDocFreq=5,wordLengths = c(3, 3),bounds = list(global = c(5,Inf)),weighting = weightTf,encoding = 'UTF-8')
doc.tdm3=TermDocumentMatrix(doc8,control3)
# 这里截取词频高于5长度为4的词
control4=list(minDocFreq=5,wordLengths = c(4, 4),bounds = list(global = c(5,Inf)),weighting = weightTf,encoding = 'UTF-8')
doc.tdm4=TermDocumentMatrix(doc8,control4)
# 这里截取词频高于5长度为5的词
control5=list(minDocFreq=5,wordLengths = c(5, 5),bounds = list(global = c(5,Inf)),weighting = weightTf,encoding = 'UTF-8')
doc.tdm5=TermDocumentMatrix(doc8,control5)
# 得到词频列表
library(slam)
freq <- rowapply_simple_triplet_matrix(doc.tdm,sum)
freq2 <- rowapply_simple_triplet_matrix(doc.tdm2,sum)
freq3 <- rowapply_simple_triplet_matrix(doc.tdm3,sum)
freq4 <- rowapply_simple_triplet_matrix(doc.tdm4,sum)
freq5 <- rowapply_simple_triplet_matrix(doc.tdm5,sum)
# save(freq,freq2,doc8,file ='constellation.RData')
# 验证齐普夫定律
order <- order(freq[order(freq,decreasing = T)],decreasing = T)
freq0 <- freq[order(freq,decreasing = T)]
order2 <- order(freq2[order(freq2,decreasing = T)],decreasing = T)
freq20 <- freq2[order(freq2,decreasing = T)]
order3 <- order(freq3[order(freq3,decreasing = T)],decreasing = T)
freq30 <- freq3[order(freq3,decreasing = T)]
order4 <- order(freq4[order(freq4,decreasing = T)],decreasing = T)
freq40 <- freq4[order(freq4,decreasing = T)]
order5 <- order(freq5[order(freq5,decreasing = T)],decreasing = T)
freq50 <- freq5[order(freq5,decreasing = T)]
# 结果可视化
# plot(log(order)~log(freq0))
png('logzipfplot.png')
par(mfrow=c(2,2))
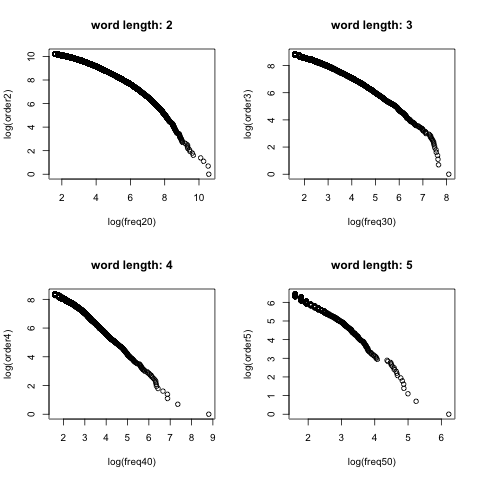
plot(log(order2)~log(freq20),main="word length: 2")
plot(log(order3)~log(freq30),main="word length: 3")
plot(log(order4)~log(freq40),main="word length: 4")
plot(log(order5)~log(freq50),main="word length: 5")
dev.off()
png('czipfplot.png')
par(mfrow=c(2,2))
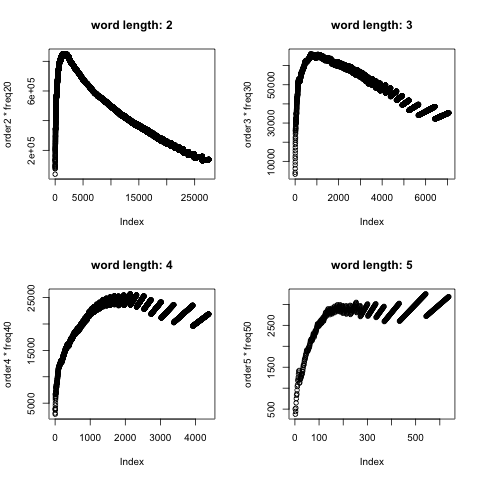
plot(order2*freq20,main="word length: 2")
plot(order3*freq30,main="word length: 3")
plot(order4*freq40,main="word length: 4")
plot(order5*freq50,main="word length: 5")
dev.off()
现象描述与讨论
结果很意外,我在很多帖子中看到人们肆无忌惮的使用该定律作为论据,但事实上且不论这本来就是一个经验定律,从我对微博数据分析的结果上看,齐普夫定律似乎并不符合微博语言习惯。
理论上第一张图会都是直线,但只有我们把词按5个一组进行区分时才能勉强看到一条直线。如果看下前50个词我们会发现这种分法可能捕捉到的更多是英文单词,所以可能是微博中大量出现的英文反映了齐普夫定律的语言使用环境。
zynga 发展中国家 happy phone
504 189 148 131
webos china 南京大屠杀 party
130 125 119 108
gmail world store style
106 104 98 98
个人所得税 ilook never there
93 90 89 88
gucci 高尔夫球场 touch adobe
81 79 59 57
weico weibo hello rovio
57 56 53 53
heart 印度尼西亚 icann green
50 49 49 47
belle kitty leave 人民检察院
46 45 45 44
原教旨主义 first light 毛泽东思想
44 44 44 43
中国科学院 black david kevin
42 42 42 42
brian yahoo 中央气象台 nexon
41 41 40 40
nexus apple muddy still
40 39 39 39
would ralph
39 38
但其实当分词在两三个时,出现的更多是中文词汇,这时候反而偏离了齐普夫定律,更像个抛物线规律。
两个字一个词
中国 腐败 城管 一个 北京 微博 问题 政府
38951 37655 28787 24242 15834 14984 12972 12651
社会 今天 美国 国家 工作 公司 经济 已经
11418 11310 11264 11261 10326 9722 8402 8227
现在 时间 表示 事件 香港 发现 世界 发生
8222 7941 7913 7755 7710 7466 7258 7196
进行 知道 人员 安全 生活 目前 新闻 调查
7189 7184 7077 7032 6985 6916 6901 6378
记者 今年 孩子 市场 官员 昨天 事故 企业
6043 6037 6034 5944 5919 5809 5748 5706
看到 图片 朋友 部门 视频 成为 全国 认为
5614 5587 5572 5496 5440 5386 5370 5339
大学 媒体
5317 5219
三个字一个词
北京市 越来越 房地产 嫌疑人 公安局 老百姓 互联网
3266 2122 2074 2033 1928 1913 1804
公务员 候选人 联合国 公安部 人民币 电视台 消费者
1789 1747 1728 1715 1657 1620 1577
亿美元 负责人 委员会 国务院 铁道部 办公室 哈哈哈
1515 1514 1513 1457 1417 1243 1243
进一步 中纪委 第一次 派出所 开发商 ceo the
1241 1213 1125 1099 1096 1090 1068
俄罗斯 幼儿园 临时工 董事长 发言人 意味着 机动车
1054 1006 982 952 916 902 897
利比亚 大学生 you 万美元 全世界 新华社 朝阳区
821 798 796 781 766 764 762
领导人 身份证 志愿者 一个月 总经理 自行车 发布会
750 741 717 705 688 661 651
奢侈品
642
那么有人会说:你去掉了高频词,这个操作自然会导致齐普夫定律的不成立。没错,如果原本的数据集遵循齐普夫定律,那么我们去掉的高频词会导致常数C达不到。显然(我不是故意用这个词的),当排序被提前理论上会导致前面数值偏小,但不会导致后面也偏小,而应该是逼近常数C。
我们来看第二张图,如果微博数据符合齐普夫定律,那么我们应该看到一条水平线,结果出现了一个山峰,还是前坡陡后坡缓。
于是我接着探索,看下出现在顶峰的词是什么鬼:
两个字一个词
人心 阻止 一套 原文 随便 展开 男性 下次 无能 征集
421 442 422 443 420 643 421 442 422 441
中方 轻松 手中 名人 走红 审判 借贷 滋生 水果 早安
423 443 420 421 425 442 422 426 643 423
团购 森林 lt 债务 买房 观众 咖啡 环卫 遭到 警告
642 441 641 640 420 639 443 440 638 421
嘉宾 城区 火锅 争取 选项 转型 原本 姐姐 震惊 角色
425 442 422 426 423 448 444 441 424 420
军事 欧元 好多 好处 富人 商务 会长 有所 沉默 真心
443 643 440 421 425 641 422 640 442 445
三个字一个词
执行官 侦查员 著作权 原材料 总公司 see 男朋友
91 91 91 92 84 63 91
徐家汇 一口气 知情人 婴幼儿 交易日 信息化 小金库
90 92 84 63 91 90 92
针对性 lte 写字楼 中文版 lee 银行家 直辖市
84 81 63 89 80 88 83
专卖店 孙悟空 多一些 太阳能 tot 中南海 微生物
62 63 91 90 61 81 92
抑郁症 手续费 fbi 自己人 小学校 新街口 一周年
84 89 80 64 62 83 88
尼古丁 gif 从业者 国家队 一两个 演播室 芝加哥
63 61 91 90 81 84 71
星期六 玉泉营 想象力 生产力 小博士 十多年 科技界
80 64 87 92 62 89 63
债权人
60
我对着这些词想半天也没搞出个所以然,但这里谈点直觉:我认为这批词词频与排序的乘积可以用来表征其在语料库中的影响力。在符合齐普夫定律的语料库中,影响力大的词无疑就是那些高频词,但这些词其实没什么卵用:因为太常见,常规自然语言处理都会有排除高频词的步骤。那么在不符合齐普夫定律且排除掉高频词的语料库中如何寻找有代表性的词?这些词不能太常见,但又不能不常见,否则形不成规律性。我感觉上面用词频与排序乘积大的词可能是符合这一要求的词汇,它们规模不大,但极有可能在不同分组中展示出巨大差别,而这种区别很有可能稀释到广泛意义上的微博日常讨论中。
半成品结论
- 即使进行了高频词的去除,微博环境特别是中文语境也并不符合齐普夫定律
- 中文语料库中展示出的词频与排序山峰式规律可能用来筛选分组中高影响力关键词
- 微博语料库中的中英文混杂现象值得注意
- 欢迎自行探索