最近重新看了下之前对p值的笔记,突然对零假设充满了陌生感。在p值的语境里,当我们看到数据D在零假设下发生的概率低就会做出数据D不支持零假设的判断,这是一个条件概率等价替换的问题:
$$p(H0|D) = p(D|H0)$$
这个当然是有问题的,我真正关心的是零假设是否成立而不应该是数据出现在零假设下概率。而这在假设检验的设计中转化成了零假设成立下出现观察数据的概率,这里最大的不对劲在于数据D不支持零假设依然无法判断零假设是否成立。对于实验科学,我们能收集数据D,但检验零假设似乎没什么道理,零假设是来自于随机过程,我们真正关心的从来都是产生差异的过程,现在却要用随机过程来检验产生差异与否,总感觉哪里不对。
不过重读了丁鹏老师的文章后,我意识到当年Fisher搞出的统计推断的背景的女士品茶实验其实是穷举所有可能,因为品茶结果是离散的,所以穷举空间是有限的,此时发生各种情况的概率是离散的,这也就形成了Fisher精确检验的基础。这里面容易被忽视的点在于品茶实验中品茶顺序与结果是无关的,也就是形成正确答案的顺序与答案无关,也就是说如果数据D是真理,那么随机化过程不影响真理对错。
那么回到前面的问题,Fisher这个p值设计实际上巧妙的规避了$p(H0|D)$与$p(D|H0)$的区别,因为在这个离散概率的语境下,空假设提供的实际是一个虚拟的有限平行宇宙,当某个假设成立时,数据一定会支持假设而不成立时数据在有限平行宇宙里只会以很低的概率出现,$p(H0|D)$与$p(D|H0)$的讨论在这里就没意义了,虚拟的有限平行宇宙实际是给出了所有可能性空间。也就是说,产生差异这件事被零假设转化成了虚拟的有限平行宇宙,其中有一个宇宙产生了差异,那么这个宇宙下待检验的假设就可以被认为是证实的。
换句话说,Fisher的零假设是包含了所有假设在内的假设宇宙,在某些宇宙里出现某些数据是正常且合理的,但这些宇宙相比所有假设宇宙的空间非常小,那么在这些宇宙里数据背后对应的规律应该就是真实的。如果假设宇宙本来就不多(当然这个只会在离散结果的条件下出现),那么事实上就形成了统计功效不足的问题。前面我意识到的不对劲其实是误会,因为我脑子里还放着与零假设对应存在的备择假设这个东西,所以我会纠结是不是检验错了。但事实上,备择假设本就是零假设的一部分,其独特性是通过在可能性空间的低概率来表征的。从这个逻辑上看,Fisher的精确检验并不存在现在普遍使用的零假设备择假设这套体系里的问题,而且只要转化一下,Fisher精确检验一样可以用在更广的领域。
这里最大的问题在于可能性空间的低概率跟数据存在规律性需要是一个东西,这也是Fisher精确检验的核心。现在很多对p值的质疑可能来自于对可能性空间认识的偏误,对于很多人而言,可能性空间是数学意义上的无限空间,但对实验结果而言,在一定观测精度下可能性空间其实是有限的而观测的数据又是一定存在于这个空间之内的,这就导致概率低下进而我们会认为规律存在。举个例子,如果观察我开门这个动作100次,那么我每次都用右手这个事件对比$2^{100}$这个可能性空间而言概率很低但存在,这件事可能让观察者得出我是右利手的规律性结论。这里统计推断只负责告诉你概率,怎么解释是观察者自己决定的事,p值0.05就是个方便决策的阈值但统计学更关心概率怎么计算。
也就是说现在对p值的质疑是集中在后面决策步骤上的,但这个决策标准其实本来应该各个学科根据自己的学科规律可能性空间来制定,不能简单把锅甩给统计学家,毕竟他们对不同学科规律可能性空间其实并不了解。很多时候重复性不好的本质是所谓规律性在可能性空间里并不稀有,随机过程就会发生,这个时候应该做的是对规律性给出更严格的定性定量要求与描述,还有种可能就是本来就是伪规律,是噪音被当成了规律,天知道科研人员为了混饭吃会不会把其实不稀有的偶发事件当成规律来报道,这时候应该被质疑的其实应该是实验者而不是统计学决策工具。
我不太清楚后面是怎么把p值从离散分布推广到0到1之间的连续均匀分布的,但现在我倒是有兴趣看下p值本身在平行宇宙里的分布了。如果有规律的事实在实验限定的空间里发生,其p值的分布应该会与随机过程产生的p值不一样。这里我不打算采用多次随机抽样,因为此时分布事实上是已知的,此时进行随机实验其实是在假设分布存在且成立的条件下判断事实。相反,我会随机生成一组数据但保留这一组数据当成既成事实,但随机化分组过程来检验p值的分布,此时应该更符合事实存在后对假设的判断这个思路,这个应该更贴近Fisher精确检验的思想。这里我们考虑三种情况:
- 真实差异固定
- 完全是随机数
- 固定的真实差异加上随机数
第一种情况是规律完全成立;第二种是完全无规律;第三种是可观察或可测量的数据。生成三组数据后我们对其分组(简单二分)进行10000次随机化操作,然后进行t检验,记录并观察p值。
set.seed(1)
# 真实差异
x <- c(rep(100,260),rep(200,260))
# 随机差异
xr <- rnorm(520)
# 考虑误差的真实差异
xm <- c(rep(100,260),rep(200,260))+rnorm(520)
p <- pr <- pm <- c()
for(i in 1:10000){
# 随机化分组
g <- factor(sample(c(1,2),520,replace = T))
p[i] <- t.test(x~g)$p.value
pr[i] <- t.test(xr~g)$p.value
pm[i] <- t.test(xm~g)$p.value
}
# 探索p值分布
sum(p<0.05)/length(p)## [1] 0.0481sum(p<0.5)/length(p)## [1] 0.5084sum(p<0.9)/length(p)## [1] 0.8978sum(pr<0.05)/length(pr)## [1] 0.0514sum(pr<0.5)/length(pr)## [1] 0.4994sum(pr<0.9)/length(pr)## [1] 0.9014sum(pm<0.05)/length(pm)## [1] 0.0493sum(pm<0.5)/length(pm)## [1] 0.5023sum(pm<0.9)/length(pm)## [1] 0.8991par(mfrow=c(3,2))
hist(p,breaks = 20)
hist(p,breaks = 100)
hist(pr,breaks = 20)
hist(pr,breaks = 100)
hist(pm,breaks = 20)
hist(pm,breaks = 100)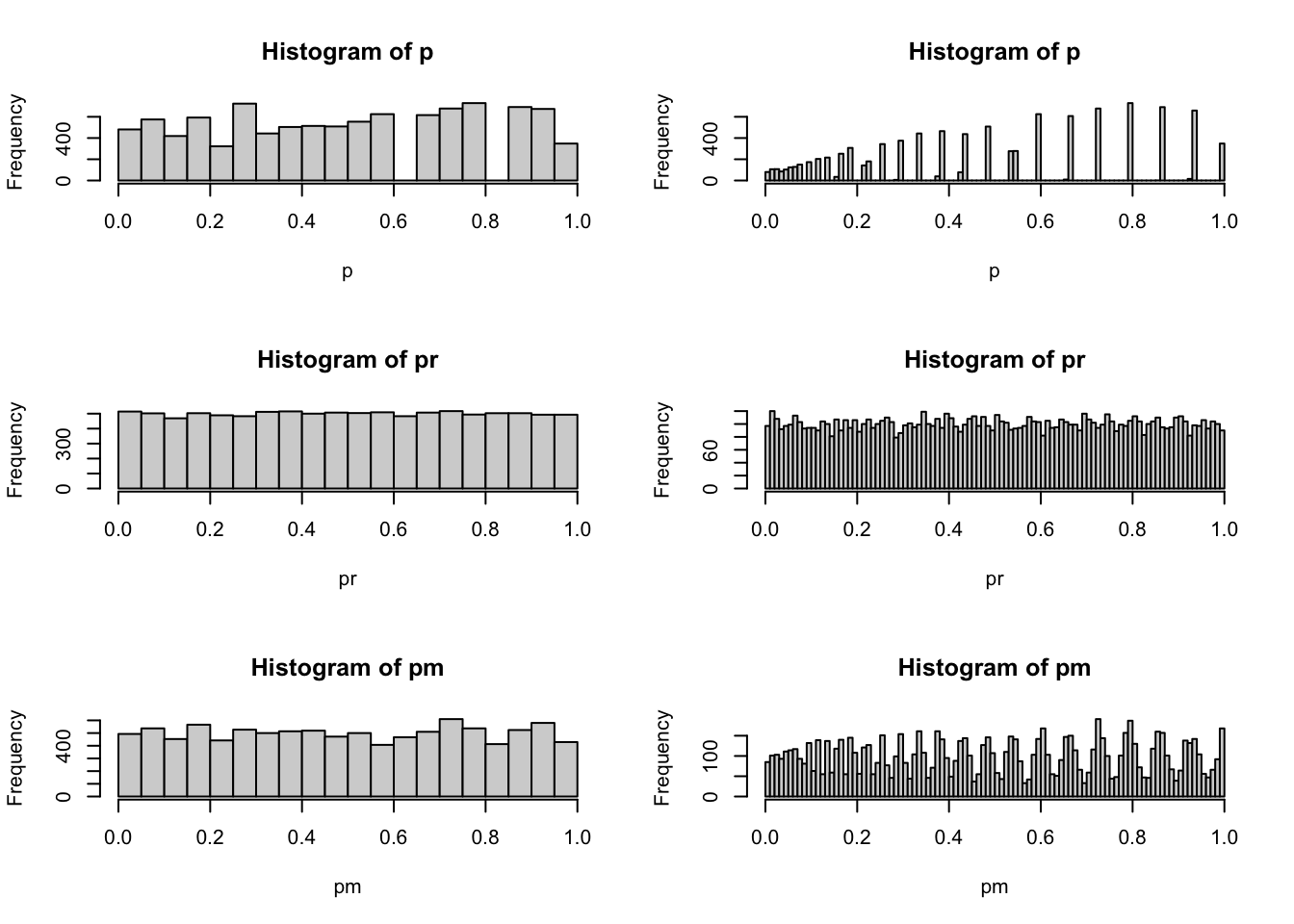
这个结果非常有意思,第一个能看到的现象是如果数据本身存在规律性,那么p值的分布是一个离散分布。这个分布介于0到1之间,越接近0的部分越密集,越接近1的的部分越稀疏,但是如果计算小于0.05,0.5,0.9的比例情况,会发现这种稀疏分布依旧符合均匀分布的概率分布特征。如果数据不存在规律性,那么p值的分布就是很均匀的。如果数据混合了规律性与噪音,依然会显示出这种离散分布特征。下面我用qq图来观察下这个分布跟均匀分布的区别:
set.seed(42)
ref <- runif(10000)
par(mfrow=c(1,1))
qqplot(ref,p)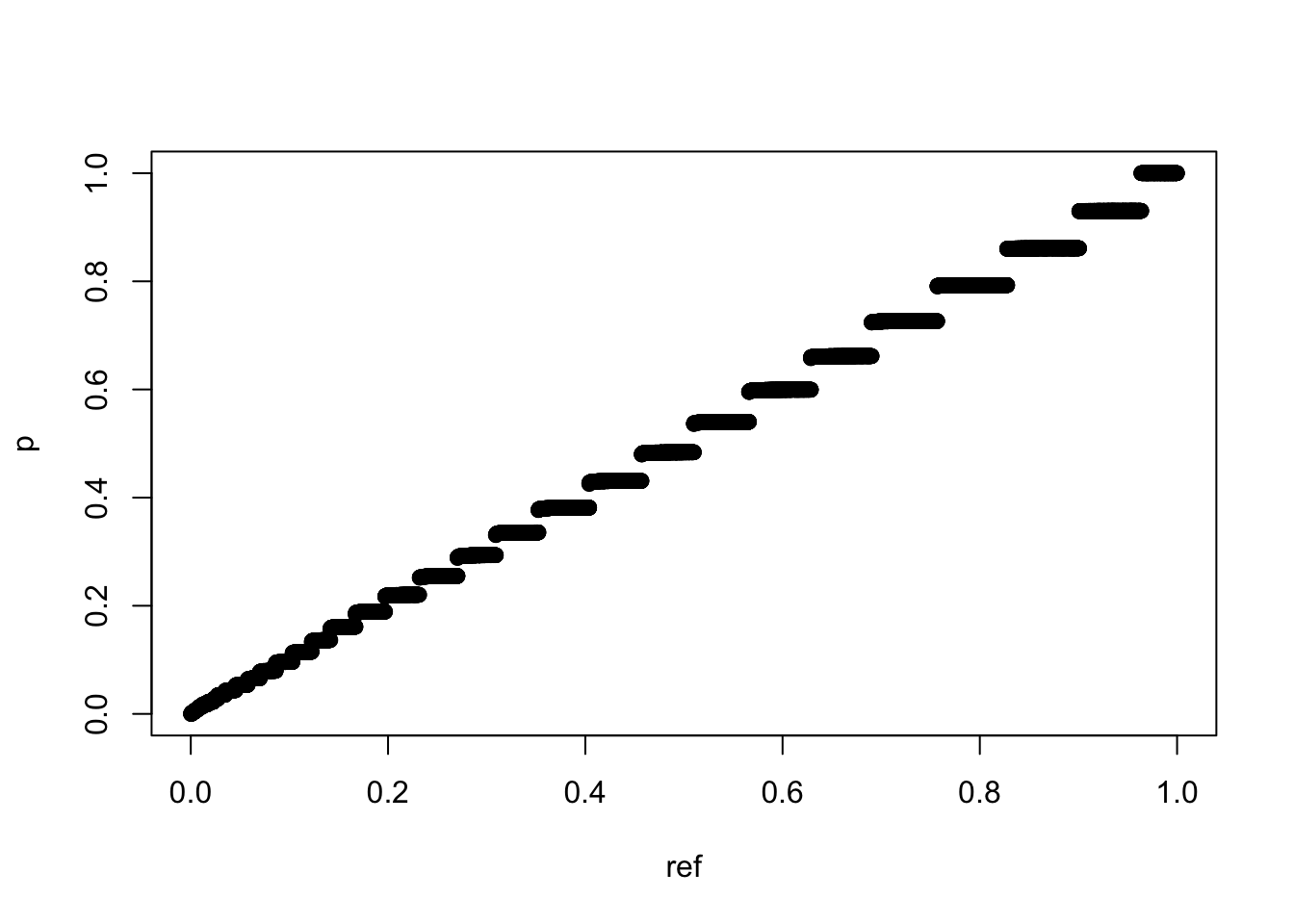
qqplot(ref,pr)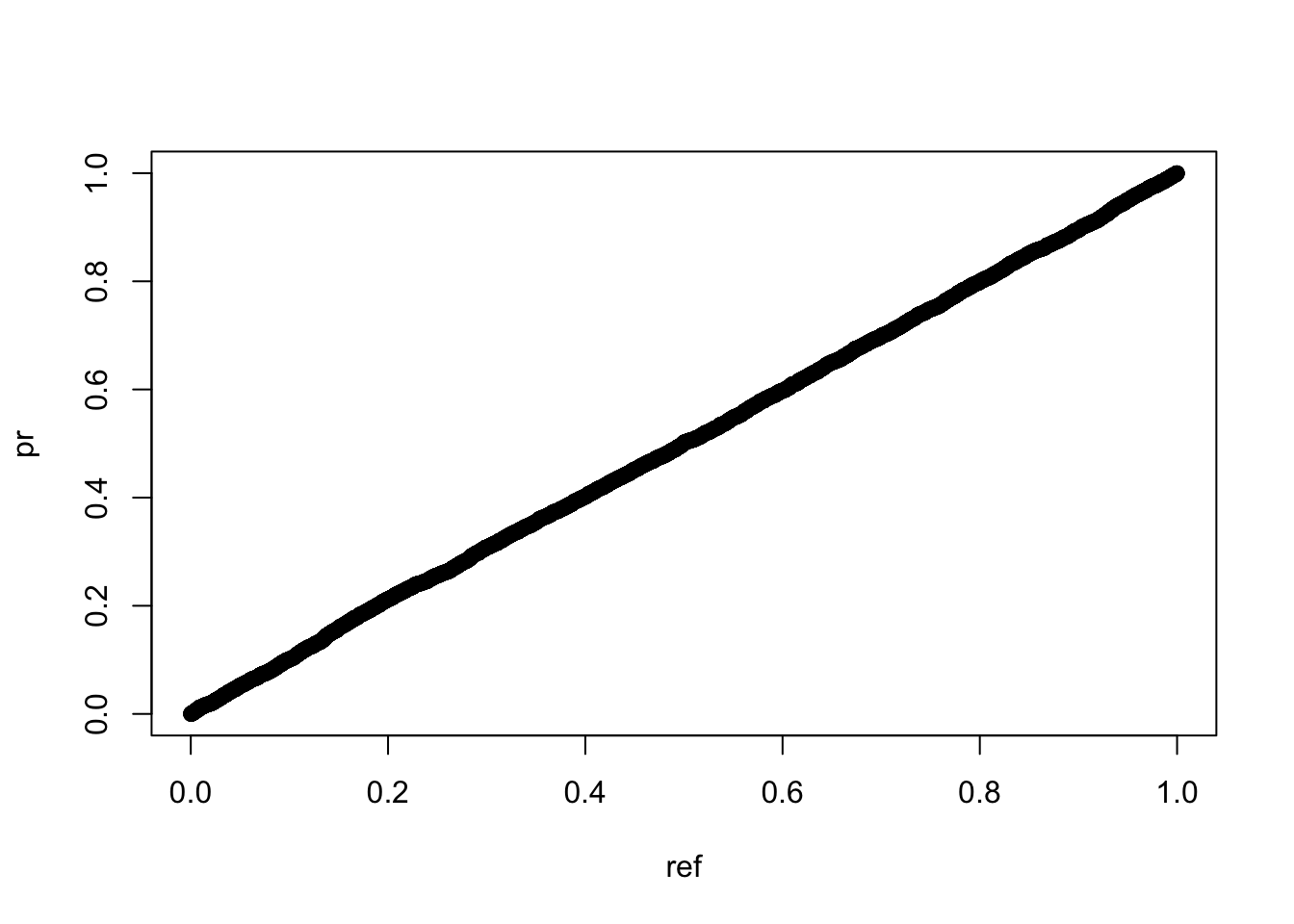
qqplot(ref,pm)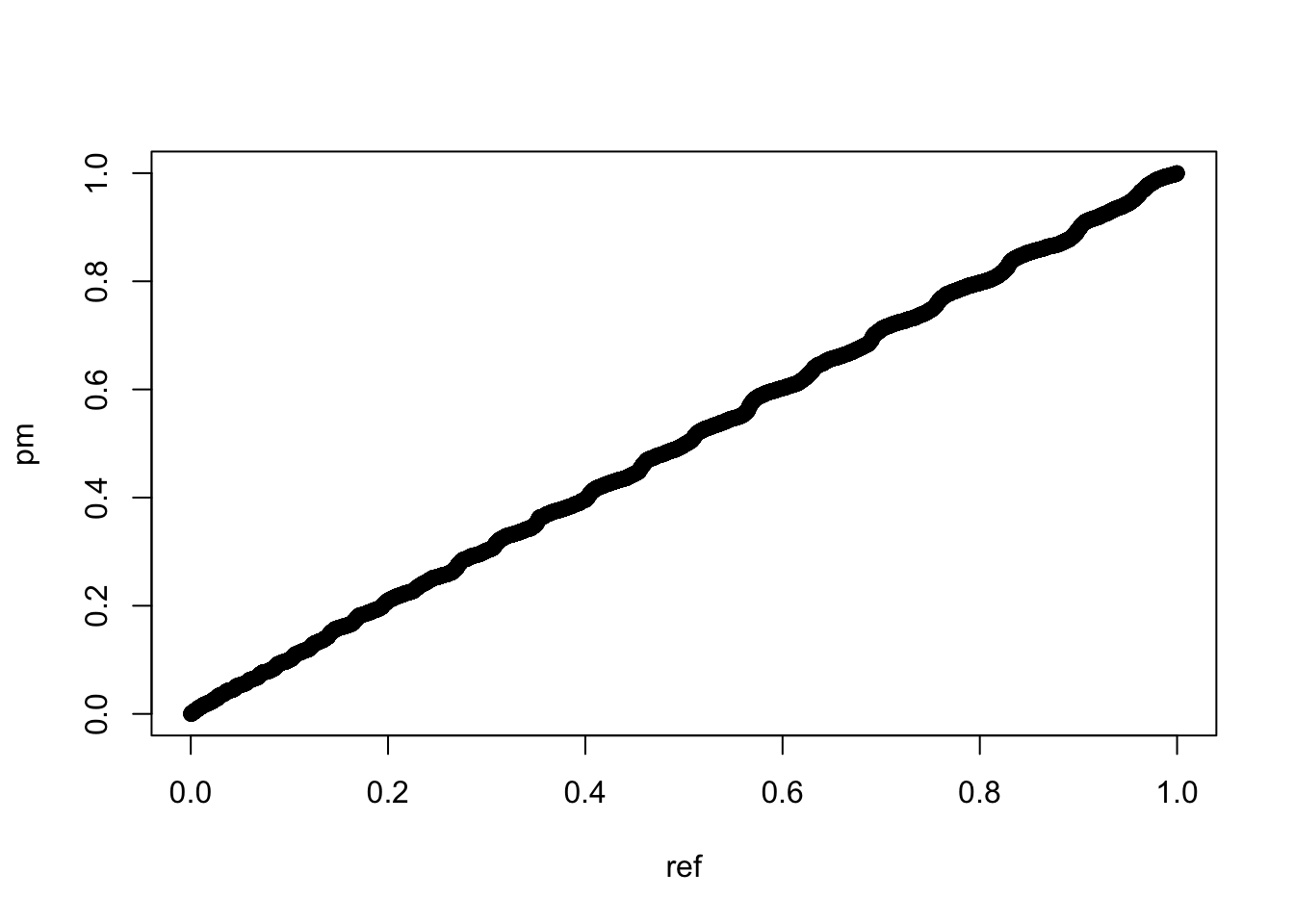
可以看到,如果数据本身存在规律性,其随机化分组后的p值虽然跟均匀分布很接近,但qq图上确实会表现出前密后舒的螺旋延伸状态。
我虽然不清楚统计学上有没有对这个p值分布的研究,如果没有我先管它叫 MY Distribution ,谁让我名字缩写就是MY,这个“我的分布”可能对实验学科非常有意义。
这里为了区别我再做一个仿真,这次我不是对分组随机而是对采样随机:
set.seed(1)
# 固定分组
g <- factor(c(rep(1,260),rep(2,260)))
p <- c()
for(i in 1:10000){
# 随机化采样
x <- sample(c(rep(100,260),rep(200,260))+rnorm(520),520)
p[i] <- t.test(x~g)$p.value
}
# 探索p值分布
sum(p<0.05)/length(p)## [1] 0.0406sum(p<0.5)/length(p)## [1] 0.5344sum(p<0.9)/length(p)## [1] 0.9356hist(p,breaks = 20)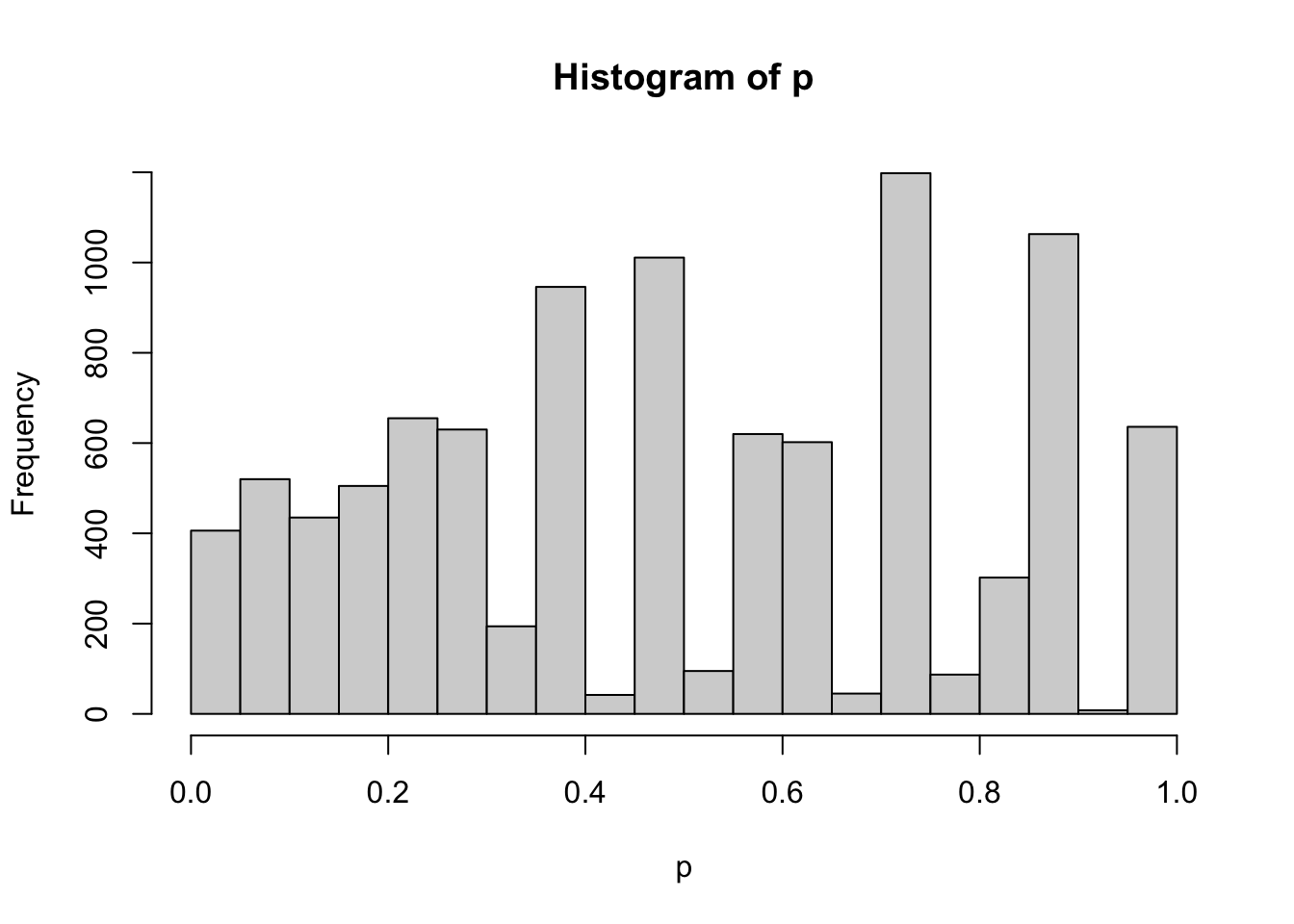
hist(p,breaks = 100)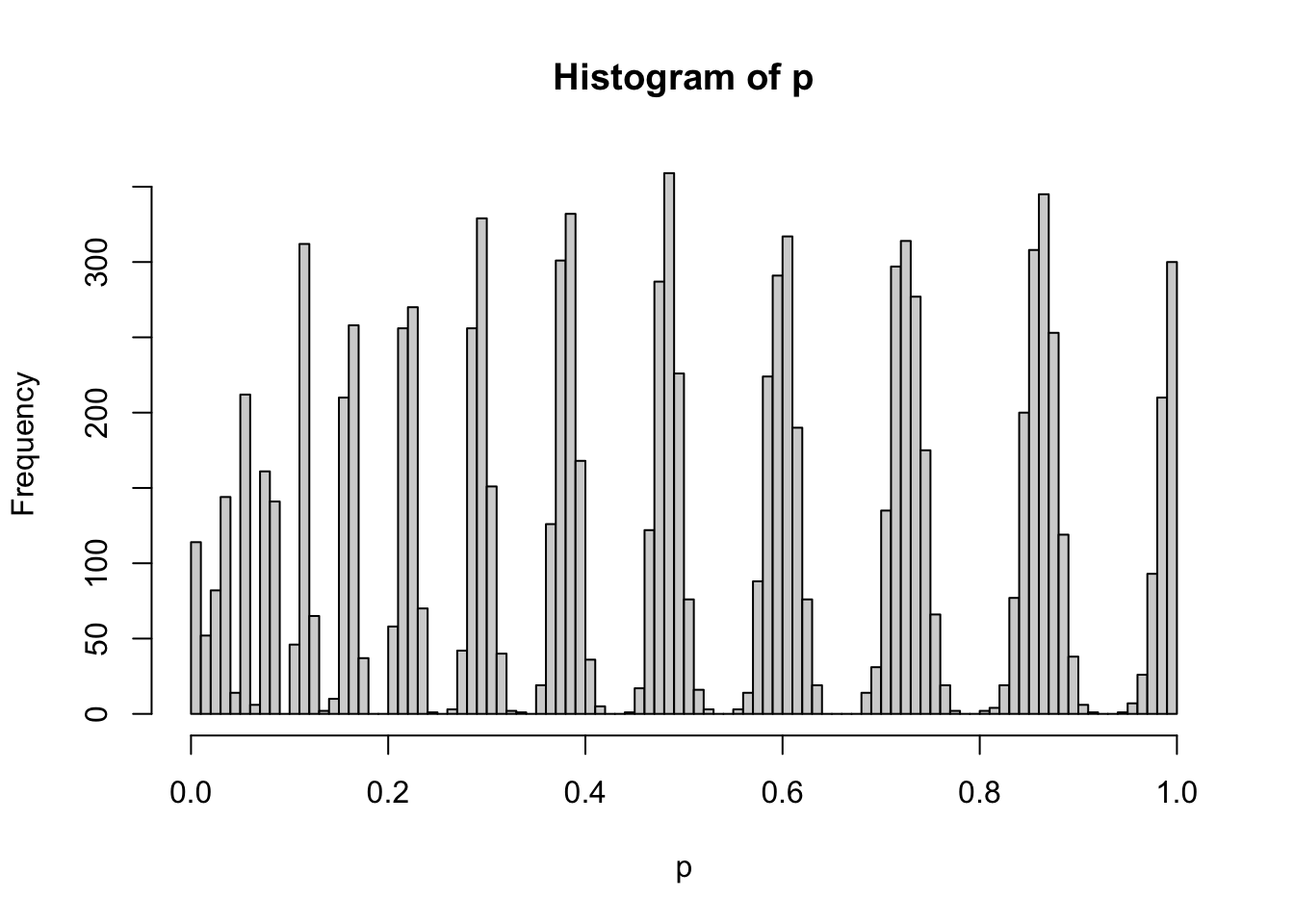
qqplot(ref,p)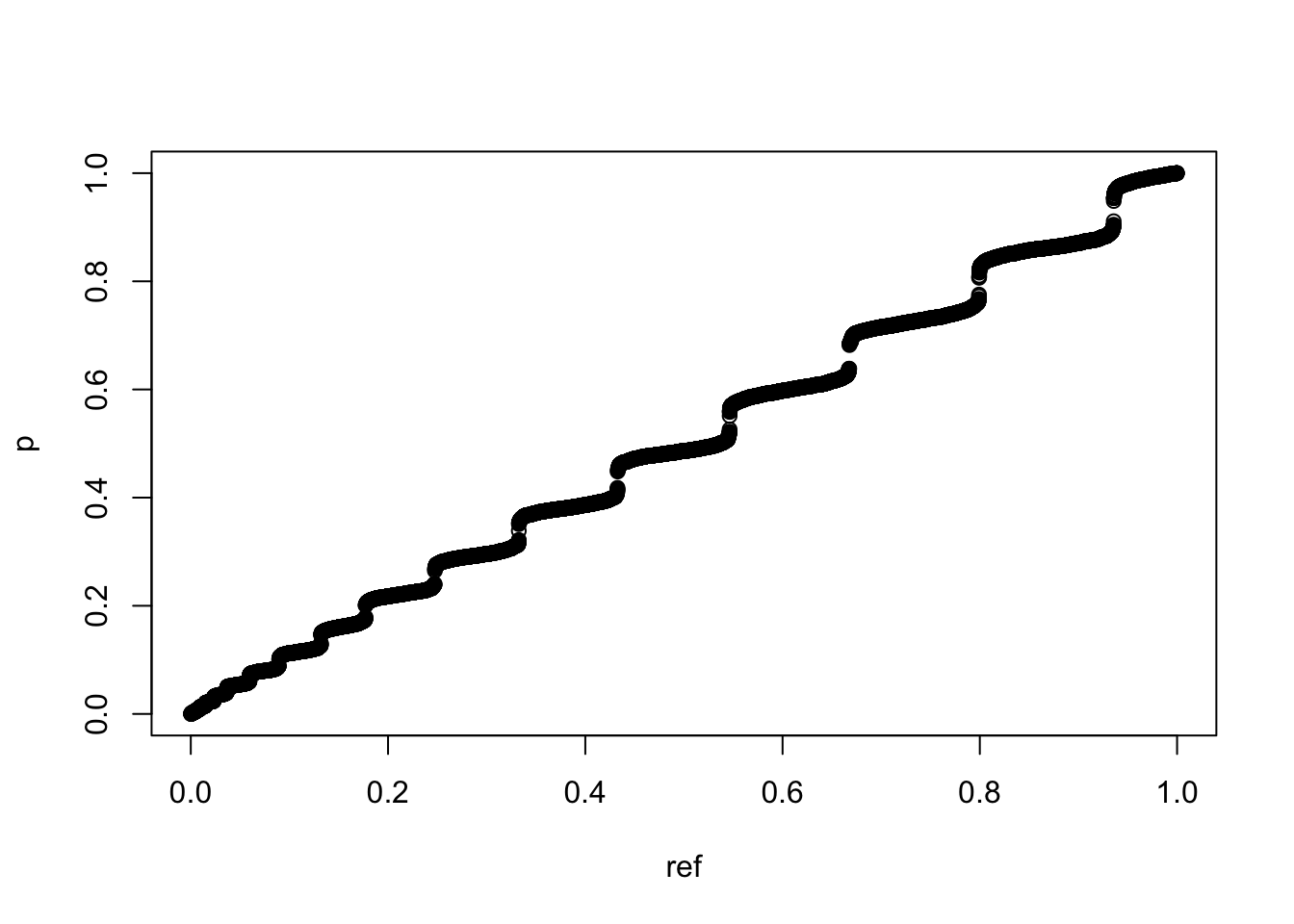
这里我们同样能看到这种蛇形走位,而且似乎随机化样品看到的趋势更明显。但同样的,这里我的模拟逻辑还是保持数据不变,只是随机化过程。
实验学科已经被多重检验问题困扰了很久了,通常演示p值分布很多人是喜欢从一个已知分布里反复抽样形成差异,此时的p值分布是有偏的:
set.seed(1)
pvalue <- NULL
for (i in 1:10000){
a <- rnorm(10,1)
b <- a+1
c <- t.test(a,b)
pvalue[i] <- c$p.value
}
# 探索p值分布
hist(pvalue,breaks = 20)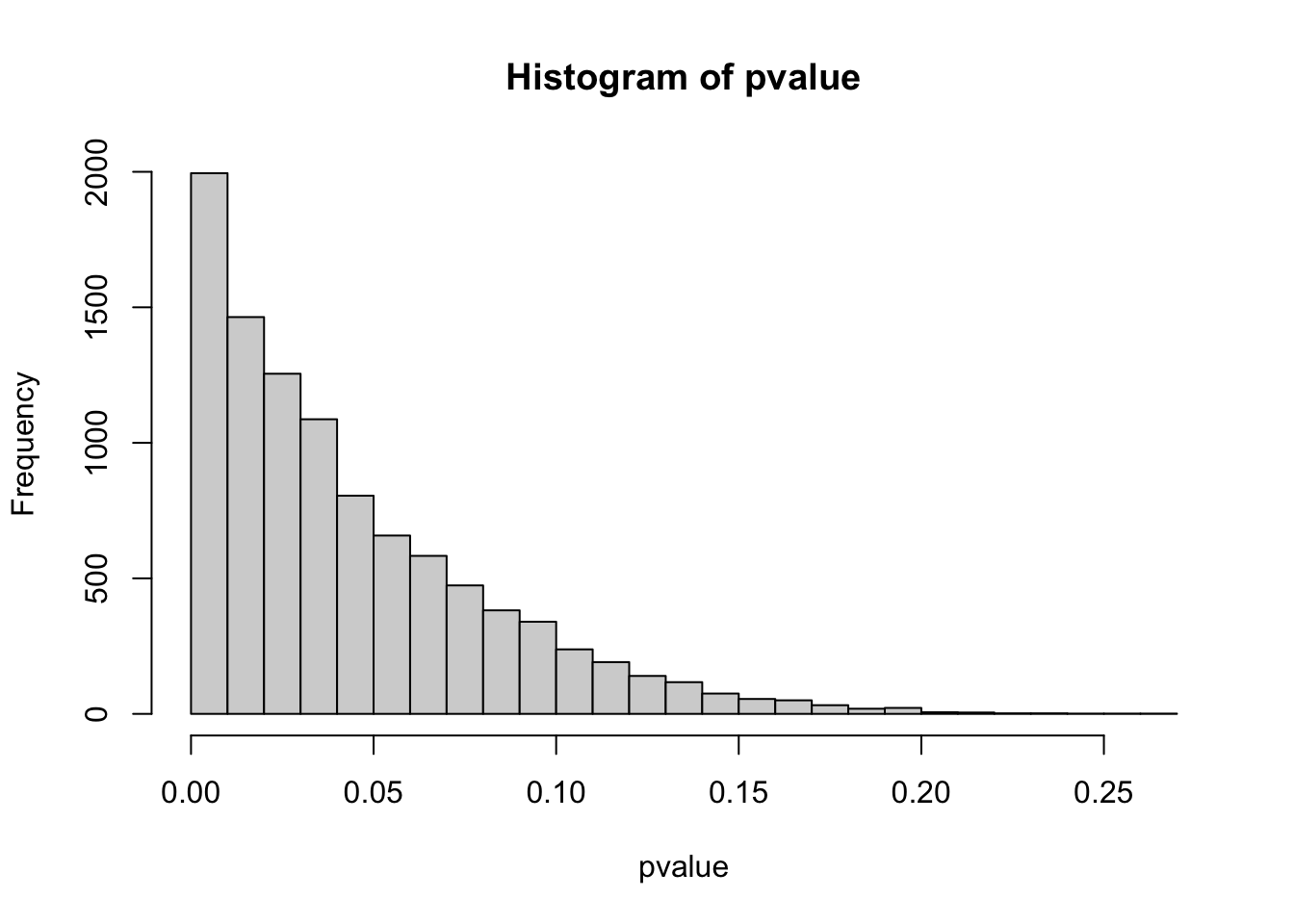
hist(pvalue,breaks = 100)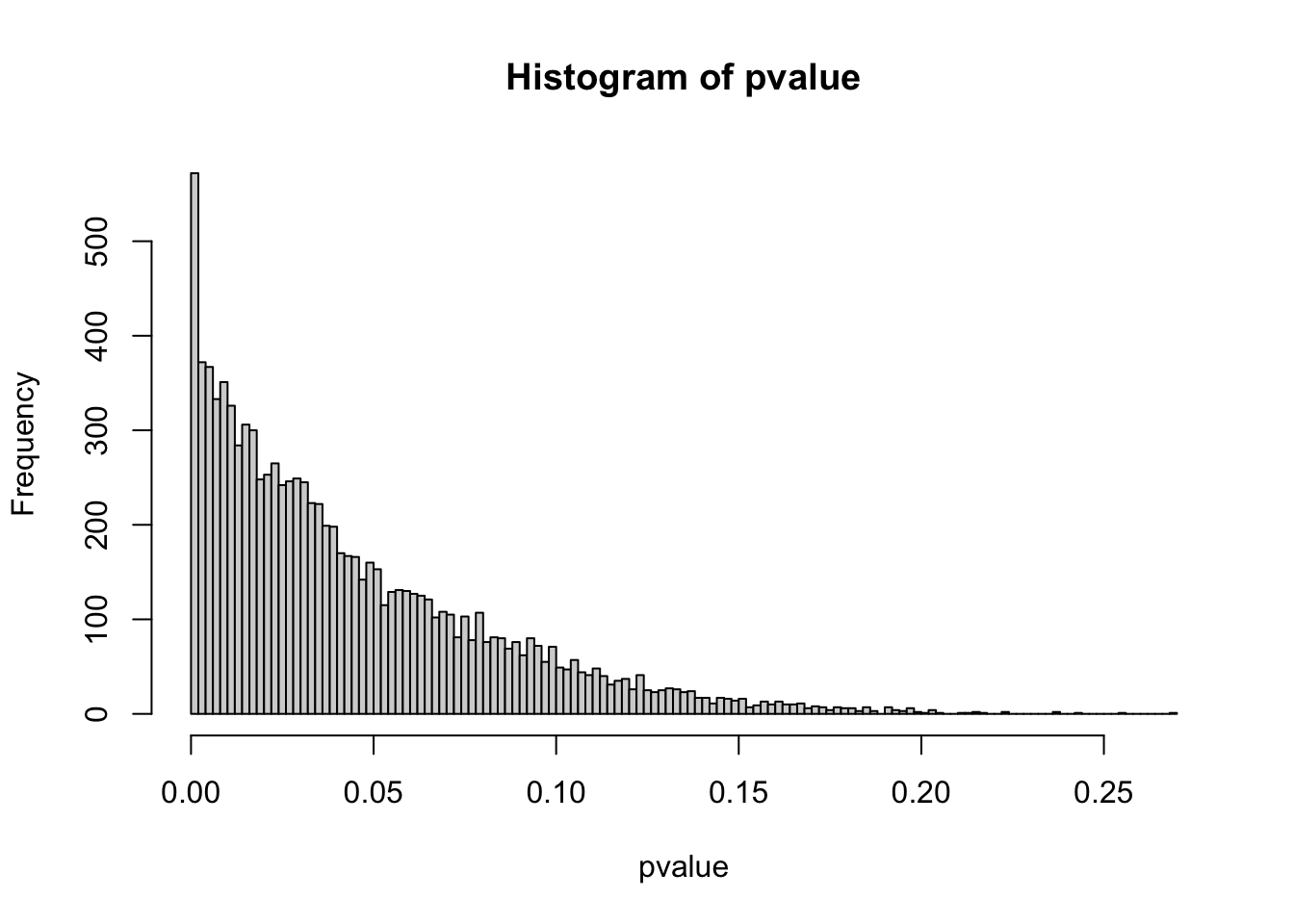
然后因为随机抽样得到的是p值均匀分布,所以很多错误发现率的控制算法都是在想办法区分这两种分布。现在常用的BH矫正、Q值法或者Bonferroni法都依赖检验数量与前面说的分布差异来决定判断标准或者控制整体错误率。这个看上去很合理,因为你检验多了出现随机相关的可能性就是高了。然而这个过程又很不合理,因为我们测量时有时候并不知道测量的维度是不是跟分组有关系,只是顺手测了,这类测量浪费了大量的统计功效。这也是传统实验学科跟组学实验学科经常扯皮的地方,传统做一对一的控制实验,如果测到了一个有意义的信号就可以发表,但技术进步后,因为我同时测了其他其实无意义的信号,那些有意义的信号被掩盖在随机相关里了。前面所说的多重检验问题的处理思想通常是保留强信号,这样本身有规律的弱信号就被自动忽略了。也许我们可以认为效应比较弱的信号不如效应比较强的信号,但只要存在规律性,作为研究人员就一定要去搞清楚是咋回事而不是用统计学工具给自己做挡箭牌。
这样,前面那个p值分布的意义就很明确了:如果规律会造成数据异质性而我们的分组过程就是试图发现这种规律性,那么不可避免的会在p值分布上造成离散分布的状态。相反,随机相关则不会呈现出这种p值的离散分布而是均匀分布。这个均匀与离散分布的差异如果能用一个统计量来描述,那么我们事实上就能根据这个统计量(暂且命名为统计量MY)区别出真实规律与随机相关。我现在能想到的构建方法非常原始,就是对直方图概率密度曲线的0.9到1这一段找最大值与最小值,如果比值超过一个阈值就认为有规律性,否则就认为是随机数据。但应该有更数学化的构建方法。
在这个语境下,我们就不用搞这些p值的阈值矫正了,直接对每一次假设检验进行分组随机化模拟过程,然后生成p值分布。如果其MY值表示为离散均匀分布,那么这一组假设检验的规律性就是有保证的,如果指示为均匀分布,那么这组数据本身就可以判定为无法检测规律而排除。这样我们可以对数据在进行统计推断前做一个规律性测试,只有通过了规律性测试的数据才值得进行统计推断。而且,只要单次统计推断给出小于0.05的p值,我们就可以直接相信,因为那些可能出现随机相关的数据已经被我们排除掉了。
不过,到这里我的知识水平已经到头了,因为这个MY值如何构建我是不知道的,现阶段我能想到的解决方案一个是直接用眼看,一个是动用图像识别的机器学习算法识别这类图像,也就是让机器看。不过这个思路应该问题不大,说白了就是利用模拟探索产生真实数据的可能性空间或平行宇宙而不是利用分布产生仿真数据,后者其实是先定在了某一种宇宙之中,这里基本延续了Fisher精确检验的思路,计算上也是可行的。
其实我也不是凭空想思考这个问题,前两天中午有个报告里演讲者提到了Fisher精确检验跟因果分析的关心,我当时忙活着做午饭没听明白她到底讲了啥,但Fisher精确检验的思想确实听明白了。然后吃着午饭就想到了这个随机化分组是不是影响p值的问题,一开始我用的是直方图的默认输出,结果发现p值总是均匀分布感到很丧气,但因为在模拟中本来是1000次多输了一个0就打算看看更精细的直方图,这才看到了这个被掩盖的p值离散分布。我应该不是第一个看到这个分布的,但将其用到替换多重检验的错误率控制上应该是个比较有前景的应用,欢迎读者来给我拍砖,要是没人写过论文(不大可能)也可以拿去写论文,我知道的已经都写出来了,欢迎引用或合作。