经常会遇到有人问条形图上误差线画什么的问题,有人说标准差(sd),有人说标准误(se),有的直接说置信区间(CI),其实这倒也不是什么大问题,你按什么画就在文章中注明就是了。后来看到JCB上有一篇科普文章,分析的比较到位,就把里面的干货跳出来翻译一下并对其中的难点进行解读,既是总结也是提高,懒得看过程可直接看文末的规则。
- 概念问题
| 误差线 | 种类 | 描述 | 公式 |
|---|---|---|---|
| 范围 | 描述性 | 极值间距离 | \(x_{max}-x_{min}\) |
| 标准差 | 描述性 | 数据点与均值的平均差异 | \(SD =\sqrt{\frac{\sum_{}^{}{(x-\bar{x})}^{2}}{n-1}}\) |
| 标准误 | 推断性 | 重复多次均值的变化 | \(SE = \frac{SD}{\sqrt{n}}\) |
| 置信区间(95%) | 推断性 | 一个有95%信心出现均值的范围 | \(\bar{x}\pm {t}_{n-1} \times SE\) |
- 标准差
标准差是描述性统计里用来表示数据本身均值范围的,两倍标准差范围以外就可能是异常值了,标准差的使用不牵扯均值对比推测,仅仅是描述性的。样本标准差会随着样本数增加接近总体标准差,可用来作为总体标准差的估计,不随样本数变化而变化。
既然随着样本数增加样本标准差与总体标准差是一致的,怎么又说不随样本数变化?
你可以这样理解,总体方差是客观存在的,我们用样本去对总体方差进行估计,具体的算法就是上面那个公式,可用点估计方法自行推导,得到的就是一个接近总体方差的数,这个数当然不会随样本数发生变化了。至于说公式,要记住伴随样本数增大,分子也在增大,所以整体上这个数是不会随样本数发生变化,毕竟只是一个估值无偏性的问题。
- 标准误
置信区间是针对均值自身而言的,是对均值真实值出现范围的估计,在这一范围内每个点都可能是真值,在置信区间的计算中也会用到标准误。因为涉及均值出现范围,一般就会涉及均值比较与估计的问题,谁比谁大或小,是否显著,这属于推断性统计。置信区间与样本是相关的,越大越不准,越小表示准确度高(样本数自然要大一些)。在使用这类误差线时要考虑自己是否有此意图。
95%置信区间中样本平均值的地位
这个95%的置信度可以用仿真实验来掩饰,谢益辉写的R扩展包animation中conf.int()可以很清楚的演示这一过程:不断从总体中取样并计算95%置信区间,重复n次,最后统计区间包含总体均值的概率你会发现有95%的区间包含的真值。区间包含真值的概率是95%,而不是真值在这个区间里变动,计算出的置信区间可能不包含真值,毕竟置信度为95%。样本的均值是没有固定位置的会跟着取样走,但总体均值不会乱跑,因为不知道,所以用含有置信度的区间估计会更可靠一些。
标准误与置信区间的区别
看公式就知道了,标准误跟着样本数走,样本数越大,标准误越小,很多文章会使用MSE,这代表了均值的标准误。应该说重复越多,这个数就越压缩均值出现的范围,一般而言都是样本数为3,不是因为多了不行,而是说3个样本可以说明问题,有条件当然样本多了好了,结果会更准。置信区间还涉及一个t值的问题,在样本数较少例如3的时候,t值比较大,约为4,样本数多于10,一般就是2左右了。置信区间在一定程度上对样本数不如标准误敏感,给出MSE与样本数是可以推测置信区间的,样本数为3就是4倍MSE,为10就是3倍MSE。
如何利用置信区间来判断显著性
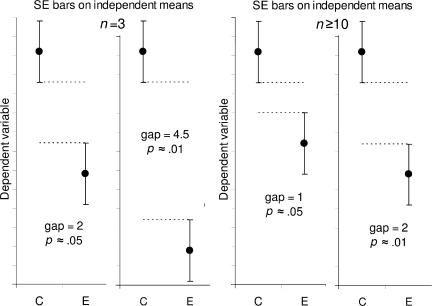
置信区间是统计估计问题,显著性是统计推断问题,这是首先需要分清楚的,然后看下面这个来自原文的图就很清楚了。通过间距判断就可以,这里需要纠正的问题就是一定要间距完全分开才有显著性差异,根据情况来。
alt text
alt text
- 样本数
使用样本数要注意你是一个样本重复测定n次,还是n个样本测定1次。前者表示同一样本,n实际为1,后者表示独立样本,样本数为n。如果你展示的是一组代表性独立数据,那就不用给出重复测定误差线,这对总体推断没多大意义。
实验设计中的可重复性究竟指的是什么?
一个实验设计三个平行,重复了4次,那么n应该是多少?n为4,因为这4次测定是与你要检验的假说有关的,那三个平行取均值就可以了,作为对数据真实性的保证。保证数据可用与重复性是两个概念,这一点是经常被混淆的。有人做实验重复了10次发现其中有1次结果是可用的就用这组数据去写文章,里面实际只有平行,没有重复。实际的科研是要考虑这10次结果的,当然前提是每次实验所有操作都是一致的,只用一组数据去写文章是碰运气,可以说完全没有重复性,这里每一次重复代表获得一次独立样本。当然这也分情况,根据你的题目自行考虑。
如何表示重复测量数据?
做分析的会比较关注,组内重复测量数据对于组间比较是没有意义的。例如在暴露实验中,同一时间点的数据带有误差线的暴露组与对照组是可比的,但是不同时间点的数据置信区间就没什么意义了,或者你可以用配对t检验差值的方法来考虑同一组内不同时间点测定区别是否显著。一般遇到这个问题都是考虑影响因素的时候,最好每个因素单一考虑,当然你也可以设计正交实验。重复性与独立性是相对的,根据你的实验设计来决定。
规则
- 使用误差线要注明种类
- 要注明样本数n
- 误差线与显著性只用在独立重复实验上,代表性的实验结果不应该包含误差线与P值,因为这相当于n=1
- 推断性实验的误差线最好使用标准误或置信区间,对于n为3的实验,可直接列出3次的结果,不标注误差线
- 95%置信区间表示有95%信心里面有总体的均值,n为3时,标准误的4倍为这个区间
- n为3,两倍标准误不重复覆盖,P < 0.05, 刚好覆盖,P接近0.05;n大于10,间距1倍标准误,P接近0.05,两倍就是0.01
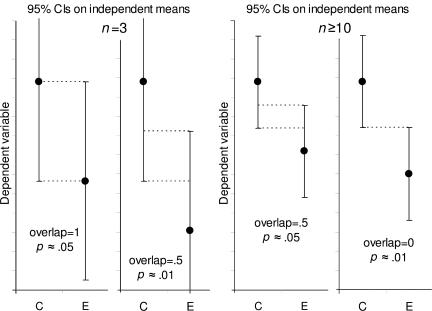
- 置信范围表示误差线时,n为3,重叠一臂,P为0.05;重叠半臂,P为0.01
- 同一组内的重复实验,标准误与置信区间不能用来表示组内差异
原文:Cumming G, Fidler F, Vaux DL.Error bars in experimental biology.J Cell Biol. 2007 Apr 9;177(1):7-11.