探秘公钥与私钥

什么是密码

这个问题似乎很简单，密码学里密码（cipher）就是用来加密与解密的运算法则。一般使用时，密码（cipher）跟暗语（code）是差不多的，但在古典密码的范畴里，code更多指利用codebook解读的无规律语句，而cipher则强调存在相应的运算法则。

密码的分类

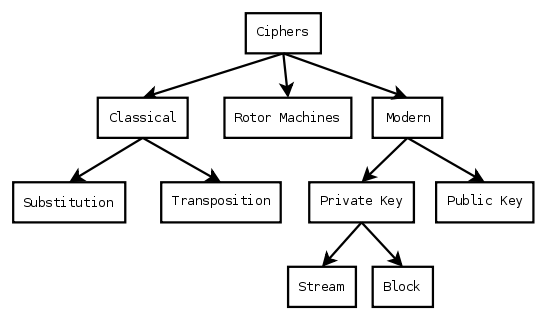
如下图，密码被分为古典密码与现代密码，至于中间的那个Rotor machine是用来解决流密码的一种机械解码装置，算是古典密码的一种，因为区别古典密码与现代密码的最主要方式就是看密码的表示方式是否是二进制的。古典密码主要采用移位与替换来实现加密与解密，众所周知的凯撒密码就是一种移位密码；现代密码主要包括私钥加密技术与公钥加密技术，其中私钥加密技术本质上与古典密码差不多，加密解密的key是一致的，但公钥加密技术就不一样了，其加密与解密的key是不一样的。这就是今天所要讨论的问题，这样的加密机制是什么。

密码的有效性

在讨论公钥加密机制之前，有必要先讨论下密码的有效性问题。众所周知，密码是用来保密的，如果很容易被第三方解密那就没什么意义了，那么密码是如何保证自己不被破解呢？首先，密码可以借用随机数来实现，但这里提到的随机数必须是真随机数而不是由函数提供的伪随机数，例如费纳姆密码就是采用明文加随机数来实现，shannon就证明过理论不可解的密码的key必须至少与明文一样长而且要加入随机数，但因为随机数实际上往往并不随机，所以事实上存在被破解的可能；其次，密码可以通过庞大的运算量来实现，换句话说就是解密的成本（如时间或运算量）过大，而明文时效性有限，这样基于实际上解密的不经济性而提供的密码正是当今使用的主流；最后，上面两种问题如果不考虑技术限制都可能被破解，这其中一个重要的原因就是明文代入的规律性，也就是说，密文带有明文的统计信息或自然语义信息越多就越有可能被破解，但另一方面，如果密文没什么规律而明文又是有规律的那这种加密方式本身事实上就是包含了明文，这样的加密方式并不具备通用性因而意义也不大，爱伦坡的小说中就出现过一个密文全是i的信，这样的密码解起来自然就不太可能了。为了实现密码的有效性与通用性，私钥加密技术就出现了，例如DES算法、AES算法……这类算法虽然不错但推广时会发现如果两个人用所需要的key还少一些，但在互联网上，数以亿计的用户如果在实现通信时互换key，且不说这个过程有多麻烦，单是key的数量就是天文数字，因此公钥加密技术出现了。

公钥密码加密的理论基础

关于公钥密码的表现形式，请参照阮一峰的博文。这里要谈的是为什么加密与解密不用同一把钥匙。

直觉上，加密与解密是互逆过程，也就是说算法也应该互逆。现代密码中采用2进制通讯，所以这类算法至少对二进制互逆，最常用的莫过于XOR算法。这类算法的实现就是对比明文与key的二进制代码，数值一致则密文为0，否则为1；这样解密时就简单多了，同样的key去对比，明文是1，key是0则密文为1，解密出的明文也还原为1。当然这说的是不包含其他算法的加密解密，但过程上只要可逆，我们直觉上就更易接受。

在公钥加密中，主要采用了单向函数。通俗地说，单向函数的意义就在于逆向运算困难，这里主要采用的是素因数分解与离散对数两种运算。

• 素因数分解。这个不难理解，给你一个数，例如42，你可以规定是通过2×3×7得到的，但它也可能是6×7得到的，对于小数字似乎不明显，但对于一个大数而言例如1675401，你能看出来是3×7×19×19×13×17得到的吗？如果里面的素数因子越大，这样的反算就越困难。但相反的，如果你知道数m的n-1个因子就很容易得到另一个未知的因子，这就是key，也就是攻克单向函数的单向陷门函数。

• 离散对数。如果你知道\[a^b=c\]这个公式中的a与b，那么c很容易就求出来了，但如果知道的是a与c求b就悲剧了，这就是离散对数问题。

那么这些运算方法如何运用在公钥加密里的呢？以RSA算法为例讲解的话，就要了解下取模运算，取模运算可以保证数n的运算结果只出现在1～n-1之间，且也能保证四则运算都可以进行，这对于擅长处理有限域问题的计算机而言是十分有利的。那么取模运算又是如何与上面的素因数分解结合在一起的呢？这就依赖费马小定理了，如果两个数a与n互素的话，那么\[a^{n-1}!=1 (mod n)\]。但事实上，费马小定理判定出的数不见得就是素数，如3215031751这个数在a=2，a=3，a=5，a=7上是满足费马小定理的，但这是个伪素数（151×751×28351）。但在实际应用上是可以接受这种误差的，所以这个问题到不用太纠结。事实上，费马小定理只是欧拉定理的一个特例，而a的欧拉函数（只小于n与n互素的数的数量）次方对n取模都得1，所以我们可以看到事实上在1到n-1的所有所有整数上，有

\[a^{kL+1}=a(mod n)\]

其中，L是\(n=pq\)中(p-1)与(q-1)的最小公倍数，k为非负整数

那么对于RSA算法而言是如何利用这些规律的呢？

首先，加密的表示是\(C=P^e(mod N)\)，这里P是明文，C是密文，e N都是公钥；解密的表示是\(P=C^{d(mod N)}\)，其中d是私钥。将解密的公式代入会发现事实上有\(C=C^{ed(mod N)}\) ，那么这里面的问题就很明显了，只要\(ed=kL+1\)的话这一组加密与解密就成立，更重要的是，L正是素因数的最小公倍数，这就将素因数分解与加密相结合了，同时也可以发现用不同的e（公钥）可以得到不同的d，一般为了安全性e会选的大一点这样对应的d也会大一些，破解起来就更麻烦。在RSA算法中，明文通过编码方式转换为二进制码，二进制码通过分组转换为10进制的数，然后通过公钥进行加密，解密的时候根据私钥计算得到明文，然后转成二进制码，之后转为明文就可以了。从这一过程可以看出事实上加密与解密的关键在于公钥与密钥一定是配对的而不是独立的。上面是用素因数分解构成的算法，实际离散对数也可以构成相应的算法，只不过还需要一个随机数来辅助。说到这里，你会发现在这个加密体系中运算量实际是很大的，与之形成对比的是私钥加密体系，其运算速度快，但问题就是发放钥匙比较麻烦，所以实际使用时往往采用hybird加密方法，也就是用公钥体系加密私钥体系的钥匙，用私钥加密大量的明文信息且一同封包传输。至于说不加密的明文传输中想知道文本信息是否被篡改，可以通过校检hash函数值来实现（毕竟不是每条信息都需要加密）。如果还不放心，可以用依赖私有钥匙的hash函数来校检。再不放心就要用电子签名了，这一点在阮一峰的博文里提到了就不赘述了。

公钥的应用实现

前面扯了一些基础，可能你会奇怪，这么复杂的过程怎么感觉不到呢？其实很容易感觉到，我们需要的是有公信力的第三方颁布的公钥证书而已。当我们浏览加密网页时，服务器传输的事实是用自己私钥加密过的密文与证书，而我们的浏览器需要做的就是通过证书管理器来校检这证书是否靠谱，不靠谱就会提示错误而靠谱就会用证书里的公钥与服务器通讯。KK在《失控》里提到加密必胜，并认为这是节制互联网无限链接的法宝，没错，无规矩的自由是混乱，有隐私的互联才会稳定。