眼下正是登高望远的好时节,但这些日子疲于实验懒得动弹便打算宅过劳动节,只是身体不动的话脑子就闲不住了,想来想去觉得这个登高究竟能看多远是个有意思的问题便简单计算了一下。
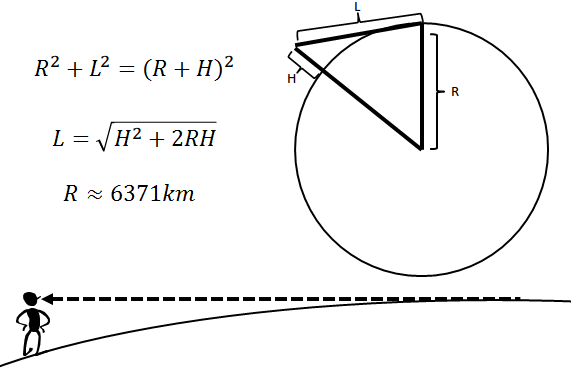
如上图,如果我站在海边,眼前没有遮挡物,那么我所能看到的距离便如同图中L所示,我的视点高度大约170cm,也就是说我所看到的地(海)平线实际据我的距离大约是4.6km。换句话说,对多数人而言,地平线在其4~5km的地方,但这里的前提是在海边,当然,人类的聚居点也大都靠河或海。
但如果你打算登高情况就不一样了,从L的计算公式来看,当H远小于R时(计算你站在珠穆朗玛峰的顶端,H也不过是约9km),$$\sqrt(2RH)$$提供了主要的距离,为此其实可以将公式经验化为L等于$$113\sqrt(H)$$。这样如果我们打算看到“千里目”,我们的L大约是500km(按照唐代度量衡来计算可能略大于这个数,约530多公里),换算一下,我们需要站的高度是19.6km。很遗憾,别说位于山西的鹳雀楼达不到,就算吧迪拜塔建到珠穆朗玛峰顶上也达不到这个高度。有兴趣可以试一下,如果我们就把楼建到珠穆朗玛峰峰顶,那我们“穷千里目”到底要上几层楼,结果是大约要建将近4000层楼(每层楼按3m计算)。像这样高度的楼根基必然要是实心的,如果将砖的承重计算进去的话,按这里的计算看,在那个年代的技术条件下,这个楼最高也就2.2km,看来即便你打算登高想要看个千里也是一件极困难的事。那就让王之涣穿越到现代又需要爬几层位于山西的楼去穷“千里目”呢?大约6000层楼,即便按现行的建筑要求加装电梯,并且是东方明珠塔那种全球最快22km/h的电梯,王先生要是到顶也需要将近一个小时。这还是建立在能造出这么高的楼的前提下。
那么下一个问题就是,王之涣究竟看了多远?鹳雀楼楼高73.9m,我们假设王之涣站在楼顶去看,得到的计算结果约是30km,也就是60里。60里也不是个小数了,就算是现在的军训,最后的拉练也就是60里路,所以王诗人的眼界还是足够开阔了。
看到这里有人可能想到,是不是我在飞机上就可以看这么远了呢?一般而言,参考下面的介绍
民航飞机的飞行高度层 中型以上的民航飞机都在高空飞行,此处的高空是指海拔7000——12000米的空间。在这个空间以1千米为1个高度层,共分为6个高度层:7千米、8千米、9千米、1万米、1万1千米和1万2千米。高空飞行的飞机只允许飞以上给定高空。 另外,民航飞机在飞行时,以正南正北方向为零度界限,凡航向偏右(偏东)的飞机飞双数高层,即8千米、1万米、1万2千米高度层;凡航向偏左(偏西)的飞机飞单数高度层,即7千米、9千米、1万1千米高度层。
我们假设飞行高度在1w米的高空,这样我们能看到的也不过357km,很遗憾,还是看不到万里。更重要的是,这还得假设天是晴朗的,否则,更可能看到的是天空中的云海及云海的海平线。下面是最近去重庆开会时飞机上看到的,其实有这种景色能不能看到千里也无所谓了。其实,类似的景色在07年泰山之巅的云海日出也很类似,胜景常有而闲暇日缺,有机会还是多出去转转吧。

那么这篇文章有没有硬伤呢?当然有,我们的视线并不是直的。换言之,我们所看到地平线事实上已经在地平线以下了,也就是说,考虑大气的折射看到千里也不是完全没有可能,只需所需的条件需要仔细演算,气温,气压,空气洁净度……也许正是这个世界的复杂才让那些诗情画意总有实现的可能,也只有了解了自己的渺小才能真正的强大。
最后,五一快乐!